Question

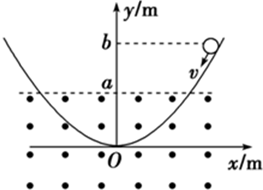竖直平面内有一形状为抛物线的光滑曲面轨道，如图所示，抛物线方程是y=x²，轨道下半部分处在一个水平向外的匀强磁场中，磁场的上边界是y=a的直线（图中虚线所示），一个小金属环从抛物线上y=b（b＞a）处以速度v沿抛物线下滑，假设抛物线足够长，金属环沿抛物线下滑后产生的焦耳热总量是（　　）

• A．mgb
• B．

  1

  2

  mv²
• C．mg（b-a）
• D．mg（b-a）+

  1

  2

  mv²

Answer 1

分析：圆环在进入磁场和出磁场的过程中产生感应电流，有热量产生，最终以y=a以下来回摆动，根据能量守恒求出金属环沿抛物线下滑后产生的焦耳热总量．

解答：解：圆环最终在y=a以下来回摆动，以y=b（b＞a）处为初位置，y=a处为末位置，知末位置的速度为零，在整个过程中，重力势能减小，动能减小，减小的机械能转化为内能，根据能量守恒得，Q=mg（b-a）+

1

2

mv2．故D正确，A、B、C错误．
故选D．

点评：解决本题的关键知道最终在y=a以下来回摆动，在摆动时无热量产生，以初始位置与y=a位置为研究过程，动能和重力势能的减小量全部转化为热量．