题目内容
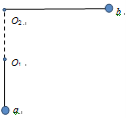
【题目】如图所示,质量为km小球a,用l1=0.4m的细线悬挂于O1点,质量为m小球b,用l2=0.8m的细线悬挂于O2点,且O1、O2两点在同一条竖直线上。让小球a静止下垂,将小球b向右拉起,使细线水平,从静止释放,两球刚好在最低点对心相碰。相碰后,小球a向左摆动,细线与竖直方向最大偏角为600,两小球可视为质点,空气阻力忽略不计,仅考虑首次碰撞。取g=10m/s2。求:
(1)讨论k可能的取值范围
(2)所有满足题干要求的碰撞情形中,k取何值时?机械能损失最多。
【答案】(1) ![]() (2) 当
(2) 当![]() 时,动能损失最大。
时,动能损失最大。
【解析】
(1)对小球b下摆过程:
![]()
得出碰前![]() ,
,
小球a上摆过程:
![]()
碰后![]()
对两球碰撞过程有
![]() ,
,
得出![]() 。
。
由碰撞过程动能不增加有:
![]() ,
,
得出![]() ,
,
此外由碰撞中合理性原则得:
![]() ,
,
得出![]() 。
。
综上所述![]()
(2)碰撞中动能损失:
![]()
可以得出当![]() 时,动能损失最大。
时,动能损失最大。

练习册系列答案
相关题目
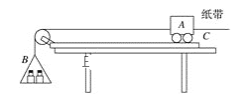
【题目】某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个测量点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为0.10,试完成下面问题。

(1)根据纸带上各个测量点间的距离,某同学已将1、2、3、5点对应的时刻的瞬时速度进行计算并填入表中,请你将4点对应的时刻的瞬时速度填入表中。(要求保留3位有效数字)
瞬时速度 | v1 | v2 | v3 | v4 | v5 |
数值(m·s-1) | 0.165 | 0.214 | 0.263 | ________ | 0.363 |
(2)在图中所示的直角坐标系中画出小车的瞬时速度随时间变化的关系图线________。

(3)由图象求出小车的加速度a=________ m/s2。