题目内容
 如图所示,一纸带放在水平面上,其上压一重物,现将纸带水平向右以恒定的速度匀速抽出,则( )
如图所示,一纸带放在水平面上,其上压一重物,现将纸带水平向右以恒定的速度匀速抽出,则( )分析:纸带抽出的过程中,重物在摩擦力作用下做匀加速运动,根据牛顿第二定律求出加速度,画出速度时间图象,根据位移之差等于重物的长度列式即可求解.
解答:解:对重物进行受力分析,根据牛顿第二定律得:
a=
=μg
所以重物的速度v=at=μgt
画出纸带和重物的速度时间图象,如图所示:
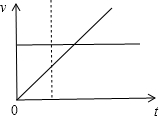
根据位移之差等于重物的长度可知,加速度越小,位移之差先达到重物的长度,所以重物与纸带间的动摩擦因数越小,抽出纸带所用时间越短,与质量无关,故C正确.
故选C.
a=
| μmg |
| m |
所以重物的速度v=at=μgt
画出纸带和重物的速度时间图象,如图所示:

根据位移之差等于重物的长度可知,加速度越小,位移之差先达到重物的长度,所以重物与纸带间的动摩擦因数越小,抽出纸带所用时间越短,与质量无关,故C正确.
故选C.
点评:本题主要考查了牛顿第二定律、速度时间图象的应用,知道速度-时间图象中,图象与时间轴围成的面积表示位移,难度适中.

练习册系列答案
相关题目

 如图所示,一纸带放在水平面上,其上压一重物,现将纸带水平向右以恒定的速度匀速抽出,则
如图所示,一纸带放在水平面上,其上压一重物,现将纸带水平向右以恒定的速度匀速抽出,则
