题目内容
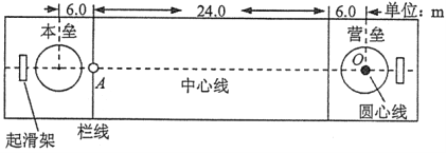
【题目】“冰壶比赛”是在水平冰面上进行的体育项目,比赛场地示意图如图,其中营垒外圆的半径为1.8m,
其余数据如图所示。比赛时,以场地上冰壶距离营垒圆心的远近决定胜负。在某次比赛中,甲队队员以v0 =![]() m. s的速度将质量m1=19kg的冰壶从左侧栏线A处沿中心线推出,冰壶恰好停在营垒的圆心0处。乙队队员以一定的速度将质量为m2=20kg的冰壶也从左侧栏线A处沿中心线推出,冰壶滑动到0 点并和甲队的冰壶发生碰撞,碰撞后恰好将甲队的冰壶弹出外圆,而乙队的冰壶向前滑行到距0点0.45m处停止。设两个冰壶均可看成质点且碰撞前后均沿中心线运动,两个冰壶与冰面的动摩擦因数相同。取g=10ms2.求
m. s的速度将质量m1=19kg的冰壶从左侧栏线A处沿中心线推出,冰壶恰好停在营垒的圆心0处。乙队队员以一定的速度将质量为m2=20kg的冰壶也从左侧栏线A处沿中心线推出,冰壶滑动到0 点并和甲队的冰壶发生碰撞,碰撞后恰好将甲队的冰壶弹出外圆,而乙队的冰壶向前滑行到距0点0.45m处停止。设两个冰壶均可看成质点且碰撞前后均沿中心线运动,两个冰壶与冰面的动摩擦因数相同。取g=10ms2.求
(1)冰壶与冰面的动摩擦因数;
(2)乙队从A点将冰壶推出时速度的大小(结果可用根式表示)。
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据动能定理求解冰壶与冰面的动摩擦因数;(2)两队的冰壶碰撞时满足动量守恒,结合动量守恒定律以及动能定理联立方程求解.
(1)甲队的冰壶滑动的位移x0=30.0m,设冰壶与冰面的动摩擦因数为μ,则:![]()
解得μ=0.01
(2)乙队从A点将冰壶推出时的速度为v1,到O点与甲队的冰壶碰撞前的速度为v2,则:![]()
设碰后甲乙两队的冰壶的速度分别为v甲、v乙,由动量守恒定律可得:
![]()
碰后甲队的冰壶滑动距离x甲=1.8m,乙队冰壶滑动的距离x乙=0.45m,则
![]()
![]()
解得![]()

练习册系列答案
相关题目