题目内容
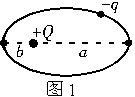
如图1所示，真空中有一固定的点电荷，电荷量为+Q，另有一带负电q、质量为m的微粒绕Q做椭圆运动，Q位于椭圆的一个焦点上，q与Q间距离最大为a，最小为b，试求q的运动周期.
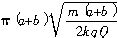
【试题分析】
直接求解q的运动周期比较困难，需用到高等数学知识，但若能联想到我们较为熟悉的行星绕太阳运动的情景，则可通过类比发现新的求解途径.考虑到由于q绕Q做椭圆运动时所受静电引力F电=k
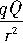与行星绕太阳做椭圆运动时所受万有引力F万=
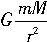在数学形式上类似，因此可推知q绕Q运动与行星绕太阳运动应遵从类似的规律.于是我们可将适用于行星运动的开普勒定律灵活迁移到本题的求解中来，即由开普勒第三定律可推知，q做椭圆运动的周期的二次方与椭圆半长轴的三次方之比为一常量，且当椭圆变为圆时，半长轴即为圆半径.因而对本题我们只需计算q绕Q做半径等于（a+b）/2的匀速圆周运动的周期就可以了，即由k
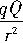=mr
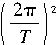及r=（a+b）/2，可解得所求周期为T=π（a+b）
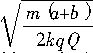
练习册系列答案
口算题天天练系列答案
相关题目
[选做题]本题包括A、B、C三小题，请选定其中两题，并在相应的答题区域内作答．若三题都做，则按A、B两题评分．
