题目内容
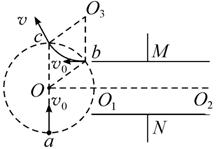
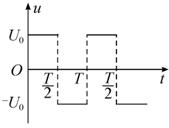
如图1所示，在真空中，半径为R＝5L0的圆形区域内存在匀强磁场，磁场方向垂直纸面向里．在磁场右侧有一对平行金属板M和N，两板间距离为d＝6L0，板长为L＝12L0，板的中心线O1O2与磁场的圆心O在同一直线上．给M、N板加上电压U0，其变化情况如图2所示．有一电荷量为q、质量为m的带电的粒子，从M、N板右侧沿板的中心线，在t＝0或t＝T/4时刻以速率v向左射入M、N之间，粒子在M、N板的左侧刚好以平行于M、N板的速度射出．若上述粒子经磁场后又均能平行于M、N极板返回电场，而电场变化的周期Ｔ未知，求磁场磁感应强度B相应必须满足的条件．(不计粒子重力)
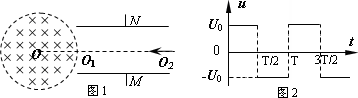
答案：
解析：
解析：
|
若要使从极板左端射入磁场的粒子又平行于极板返回电场，则它们在磁场中的运动半径r必须等于其在电场中垂直板方向上的位移y．即r＝y，否则粒子运动的情况如图所示，粒子射出磁场时其速度方向不再与中轴线O1O2平行． 对于t＝0射入电场的粒子 而 解得： 对于 若粒子在电场中运动的时间是T/2的偶数倍，则粒子沿中轴线O1O2射出电场，通过磁场偏转后，不可能再平行于中轴线O1O2射出磁场返回电场．故粒子在电场中运动的时间只能取T/2的奇数倍． 解得： 即
|
(3分)
(1分)
(1分)
(1分)
(2分)
(N＝1、2、3、……)，其中
(2分)
时刻射入电场的粒子，
(2分)
(N＝1、2、3、……)其中
(2分)
练习册系列答案
相关题目
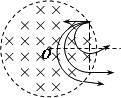
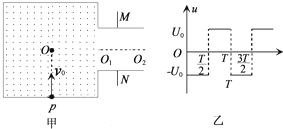如图甲所示，在真空中，有一边长为a的正方形区域内存在匀强磁场，磁场方向垂直纸面向外．在磁场右侧有一对平行金属板M和N，两板间距及板长均为b，板间的中心线O1O2与正方形的中心O在同一直线上．有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场，从正方形右侧O1点水平飞出磁场时，立即给M、N两板加上如图乙所示的交变电压，最后粒子刚好以平行于M板的速度从M板的边缘飞出．（不计粒子所受到的重力、两板正对面之间为匀强电场，边缘电场不计） 
时，该粒子从MN板右侧沿板的中心线，仍以速度v0射入M、N之间，求粒子从磁场中射出的点到a点的距离.
时刻，该粒子从M、N板右侧沿板的中心线仍以速率v0向左射入M、N之间，求粒子从磁场中射出的点到a点的距离。