题目内容
如图所示,一束光从空气射向折射率为n= 的某种玻璃的表面.试证明当入射角i=arctan
的某种玻璃的表面.试证明当入射角i=arctan 时,反射光线与入射光线垂直.
时,反射光线与入射光线垂直.

 的某种玻璃的表面.试证明当入射角i=arctan
的某种玻璃的表面.试证明当入射角i=arctan 时,反射光线与入射光线垂直.
时,反射光线与入射光线垂直.

[方法一] 如图所示,做出入射光线的反射光线及折射光线,并设反射角为
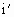 、折射角为r、入射光线与界面间夹角为θ、折射光线与界面间的夹角为
、折射角为r、入射光线与界面间夹角为θ、折射光线与界面间的夹角为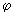 .由平面几何知识可知:当反射光线与折射光线垂直时,θ+
.由平面几何知识可知:当反射光线与折射光线垂直时,θ+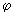 =
=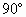 ,
,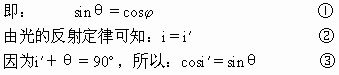
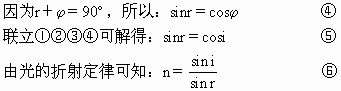
联立⑤、⑥两式并代入n的值可以解得:i=arctan

此题得证
[方法二] 在下图的直角三角形中表示tani=
 ,由三角形中的边角关系可知:sini=
,由三角形中的边角关系可知:sini=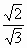
因为i=
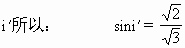

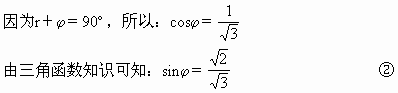
比较①、②两式可知,θ与
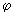 互为余角,即反射光线与折射光线垂直.
互为余角,即反射光线与折射光线垂直.

求解几何光学类型题目,运用数学知识解题及进行证明,是常用的方法.读者在进行相关计算时应充分利用题给条件,并与数学知识紧密结合,迅速把所求问题转化成三角形中的边角关系,是解决此类问题的关键.
本题是光的折射现象中的基本问题,解决本题不仅要求读者对入射角、反射角、折射角和折射率的概念清楚,而且还要根据题意正确找出各角度之间的关系,因此要求读者能对光的反射规律、折射规律灵活运用,对能力要求较高.
[方法一] 如图所示,做出入射光线的反射光线及折射光线,并设反射角为
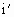 、折射角为r、入射光线与界面间夹角为θ、折射光线与界面间的夹角为
、折射角为r、入射光线与界面间夹角为θ、折射光线与界面间的夹角为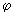 .由平面几何知识可知:当反射光线与折射光线垂直时,θ+
.由平面几何知识可知:当反射光线与折射光线垂直时,θ+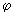 =
=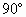 ,
,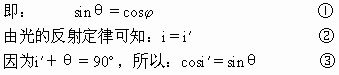
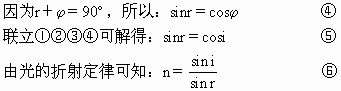
联立⑤、⑥两式并代入n的值可以解得:i=arctan

此题得证
[方法二] 在下图的直角三角形中表示tani=
 ,由三角形中的边角关系可知:sini=
,由三角形中的边角关系可知:sini=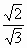
因为i=
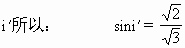

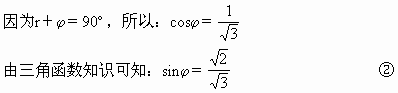
比较①、②两式可知,θ与
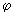 互为余角,即反射光线与折射光线垂直.
互为余角,即反射光线与折射光线垂直.入射光线与法线之间的夹角为入射角;反射光线与法线之间的夹角为反射角;折射光线与法线之间的夹角为折射角,通过审题首先应弄清楚本题所问的是哪两条光线互相垂直.介质的折射率定义为:光从真空射向介质时,入射角的正弦与折射角的正弦之比,这是解决本题的基础.
[思路一] 利用反证法及折射率的定义求解.若能证明当反射光线与折射光线垂直时,入射角为i=arctan
 即可.
即可.[思路二] 利用三角函数及折射率的定义求解.为证明反射光线与折射光线垂直,只需证明当入射角为i=arctan
 时,反射光线与界面间的夹角、折射光线与界面间的夹角互余即可.
时,反射光线与界面间的夹角、折射光线与界面间的夹角互余即可.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,然后确定圆心的位置,记在玻璃砖上
,然后确定圆心的位置,记在玻璃砖上

 的介质射入空气时,折射角r和入射角i的关系应为
的介质射入空气时,折射角r和入射角i的关系应为 d.由此得油的折射率n=_______;光在油中传播的速度v=_______m/s.(结果可用根式表示)
d.由此得油的折射率n=_______;光在油中传播的速度v=_______m/s.(结果可用根式表示)

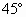 ,光束中包含两种波长的光,玻璃对这两种波长的光的折射率分别为
,光束中包含两种波长的光,玻璃对这两种波长的光的折射率分别为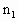 =1.5,
=1.5,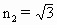 ,请回答以下问题:
,请回答以下问题:
 0的红光,从空气中垂直于三棱镜的AB面入射,从AC面射出方向如图所示.则玻璃对红光的折射率、红光在玻璃中的传播速度、红光在玻璃中的波长各是多少?
0的红光,从空气中垂直于三棱镜的AB面入射,从AC面射出方向如图所示.则玻璃对红光的折射率、红光在玻璃中的传播速度、红光在玻璃中的波长各是多少?
 ,液体中有一点光源S,上方空气中有一根很长的细杆,与液面的夹角为450,交点为A,且A点与点光源S的水平距离为0.1m,细杆与S在同一竖直平面内。要使点光源S所发生的光束照亮整个细杆,又不从A点左侧透射出水面,则点光源的深度h应满足什么条件?S所发出的光束与竖直方向的夹角在什么范围内?
,液体中有一点光源S,上方空气中有一根很长的细杆,与液面的夹角为450,交点为A,且A点与点光源S的水平距离为0.1m,细杆与S在同一竖直平面内。要使点光源S所发生的光束照亮整个细杆,又不从A点左侧透射出水面,则点光源的深度h应满足什么条件?S所发出的光束与竖直方向的夹角在什么范围内?