题目内容
20. 一辆质量为m=1000kg的赛车以某一速度进入一个水平圆弧形赛道,已知赛道半径为R=50m,(g取10m/s2)问:
一辆质量为m=1000kg的赛车以某一速度进入一个水平圆弧形赛道,已知赛道半径为R=50m,(g取10m/s2)问:(1)晴天时,赛车和路面间的动摩擦因数是0.50,若赛车的速度为15m/s,则比赛过程中赛车能否能顺利通过弯道(即不发生侧滑)
(2)雨天时,赛车和路面间的动摩擦因数是0.20,若赛车能顺利通过弯道,则赛车的最大速度为多少.
分析 根据圆周运动向心力的公式求出赛车转弯时所需的向心力大小.然后通过最大静摩擦力与向心力比较,判断赛车能否顺利通过弯道.
解答 解:(1)赛车转弯的向心力为:${F}_{n}=\frac{m{v}^{2}}{R}$.
若赛车的速度为15m/s,则:${F}_{n1}=\frac{1000×1{5}^{2}}{50}=4500$N
晴天时,赛车所受的最大静摩擦力为:fm=μ1mg=0.5×10000N=5000N.
因为最大静摩擦力大于向心力,所以赛车可以顺利通过弯道.
(3)雨天时,赛车所受的最大静摩擦力为:fm=μ2mg=0.20×10000N=2000N
赛车能顺利通过弯道的最大速度v′,有:$\frac{mv{′}^{2}}{R}=2000$N
所以:$v′=\sqrt{\frac{2000×50}{1000}}=10$m/s.
答:(1)晴天时,赛车可以顺利通过弯道.
(2)赛车的最大速度为10m/s
点评 该题考查物体做圆周运动的向心力,解决本题的关键知道汽车的水平路面上拐弯,靠静摩擦力提供向心力.

练习册系列答案
相关题目
11. 如图所示,半径为R的光滑圆形轨道竖直固定放置,小球a在圆形轨道内侧做圆周运动.对于半径R不同的圆形轨道,小球a通过轨道最高点时都恰好与轨道间没有相互作用力.下列说法中正确的是( )
如图所示,半径为R的光滑圆形轨道竖直固定放置,小球a在圆形轨道内侧做圆周运动.对于半径R不同的圆形轨道,小球a通过轨道最高点时都恰好与轨道间没有相互作用力.下列说法中正确的是( )
 如图所示,半径为R的光滑圆形轨道竖直固定放置,小球a在圆形轨道内侧做圆周运动.对于半径R不同的圆形轨道,小球a通过轨道最高点时都恰好与轨道间没有相互作用力.下列说法中正确的是( )
如图所示,半径为R的光滑圆形轨道竖直固定放置,小球a在圆形轨道内侧做圆周运动.对于半径R不同的圆形轨道,小球a通过轨道最高点时都恰好与轨道间没有相互作用力.下列说法中正确的是( )| A. | 半径R越大,小球通过轨道最高点时的速度越大 | |
| B. | 半径R越大,小球通过轨道最高点时的角速度越小 | |
| C. | 半径R越大,小球通过轨道最高点时的向心加速度越大 | |
| D. | 半径R越大,小球通过轨道最高点时的向心力越大 |
5.船要渡过一条流速稳定的小河,关于船渡河的下列说法,正确的是( )
| A. | 船头向着垂直于河岸的方向开行时,航行时间最短 | |
| B. | 船头向着垂直于河岸的方向开行时,实际航程最短 | |
| C. | 实际航线垂直于河岸方向时,航程最短 | |
| D. | 实际航线垂直于河岸方向时,航行时间最短 |
12.匀速圆周运动是( )
| A. | 速度不变的运动 | B. | 速率不变的运动 | C. | 匀变速运动 | D. | 非匀变速运动 |
9.如图(a)所示,在光滑水平面上用恒力F拉质量为1kg的单匝均匀正方形铜线框,在1位置以速度v0=3m/s进入匀强磁场时开始计时t=0,此时线框中感应电动势为1V,在t=3s时刻线框到达2位置并开始离开匀强磁场.此过程中线框的v-t图象如图(b)所示,那么( )


| A. | 恒力F的大小为1.0 N | |
| B. | t=0时,线框右侧的边两端M、N间电压为0.75 V | |
| C. | 线框完全离开磁场的位置3的瞬时速度为2 m/s | |
| D. | 线框完全离开磁场的位置3的瞬时速度为1 m/s |

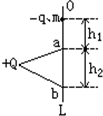 如图所示,L为竖直、固定的光滑绝缘杆,杆上O点套有一质量为m、带电量为-q的小环,在杆的左侧固定一电荷量为+Q的点电荷,杆上a、b两点到+Q的距离相等,Oa之间距离为h1,ab之间距离为h2,使小环从图示位置的O点的由静止释放后,通过a的速率为$\sqrt{3g{h_1}}$.求小环通过b点速率.
如图所示,L为竖直、固定的光滑绝缘杆,杆上O点套有一质量为m、带电量为-q的小环,在杆的左侧固定一电荷量为+Q的点电荷,杆上a、b两点到+Q的距离相等,Oa之间距离为h1,ab之间距离为h2,使小环从图示位置的O点的由静止释放后,通过a的速率为$\sqrt{3g{h_1}}$.求小环通过b点速率.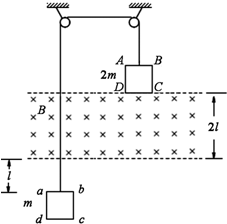 如图所示,竖直面内的正方形导线框ABCD和abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l,现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求:
如图所示,竖直面内的正方形导线框ABCD和abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l,现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求: