题目内容
15.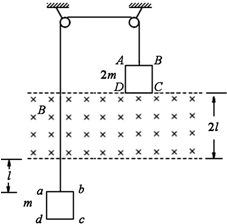 如图所示,竖直面内的正方形导线框ABCD和abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l,现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求:
如图所示,竖直面内的正方形导线框ABCD和abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l,现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求:①系统匀速运动的速度大小;
②线框abcd通过磁场的时间;
③两线框从开始运动至等高的过程中所产生的总焦耳热?
分析 (1)当ABCD刚全部进入磁场时,系统开始做匀速运动,分别对两线框列平衡方程,可得abcd框安培力大小,继而求得感应电流大小,根据欧姆定律和法拉第电磁感应定律可得系统匀速运动的速度大小;
(2)由题意可知,线框abcd通过磁场时始终以速度v匀速运动,由运动距离及速度大小可得时间;
(3)当左、右两线框分别向上、向下运动2l的距离时,两线框等高,根据能量守恒得,系统机械能的减少等于产生的总焦耳热.
解答 解:①如图所示,设两线框刚匀速运动的速度为v、此时轻绳上的张力为T,则
对ABCD有:T=2mg
对abcd有:T=mg+BIl
其中$I=\frac{Blv}{R}$
解得:$v=\frac{mgR}{{{B^2}{l^2}}}$
②线框abcd通过磁场时以速度v匀速运动,设线框abcd通过磁场的时间为t;
所以有:$t=\frac{3l}{v}=\frac{{3{B^2}{l^3}}}{mgR}$
③设两线框从开始运动至等高的过程中所产生的焦耳热为Q,当左、右两线框分别向上、向下运动2l的距离时,两线框等高,对这一过程,由能量守恒有:
$4mgl=2mgl+\frac{1}{2}•3m{v^2}+Q$
解得:$Q=2mgl-\frac{{3{m^3}{g^2}{R^2}}}{{2{B^4}{l^4}}}$
答:①系统匀速运动的速度大小$\frac{mgR}{{B}^{2}{l}^{2}}$;
②线框abcd通过磁场的时间$\frac{3{B}^{2}{l}^{3}}{mgR}$;
③两线框从开始运动至等高的过程中所产生的总焦耳热2mgl-$\frac{3{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{l}^{4}}$.
点评 本题是电磁感应中的力学问题,安培力的计算和分析能量如何转化是解题关键,要加强训练,熟练掌握法拉第定律、欧姆定律、安培力等等基础知识,提高解题能力.


| A. | 质点做匀速直线运动,速度为0.5m/s | |
| B. | 质点做匀加速直线运动,加速度为0.5m/s2 | |
| C. | 质点在1s末速度为1.5m/s | |
| D. | 质点在第1s内的平均速度0.75m/s |
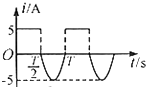 如图所示为一交变电流的i-t图象,其中每个周期的后半周期的图象为半个周期的正弦曲线,则该交变电流的有效值是( )
如图所示为一交变电流的i-t图象,其中每个周期的后半周期的图象为半个周期的正弦曲线,则该交变电流的有效值是( )| A. | $\frac{5\sqrt{3}}{2}$A | B. | 5A | C. | 10A | D. | 0A |
| A. | △vA=-△vB | B. | △pA=△pB | C. | IA=IB | D. | △pA+△pB=IA+IB |
| A. | 伽利略斜面实验合理外推解释了自由落体是匀变速运动 | |
| B. | 开普勒发现了行星运动的规律 | |
| C. | 卡文迪许通过实验测出了引力常量G | |
| D. | 惯性定律是可以被实验直接验证的 |
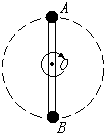 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m?,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m?,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动. 一辆质量为m=1000kg的赛车以某一速度进入一个水平圆弧形赛道,已知赛道半径为R=50m,(g取10m/s2)问:
一辆质量为m=1000kg的赛车以某一速度进入一个水平圆弧形赛道,已知赛道半径为R=50m,(g取10m/s2)问:
 如图所示,在光滑的水平面上有一足够长的质量为m1的平板小车,正以速度v向右运动,现将以质量为m2的木块无初速度地放上小车,由于木块和小车间的摩擦力的作用,小车的速度将发生变化,为使小车保持原来的运动速度不变,必须及时对小车施加一向右的水平恒力,当该力作用一段时间后把它撤去时,木块恰能随小车一起以速度v共同向右运动,设木块和小车间的动摩擦因数为μ,求这个过程中:
如图所示,在光滑的水平面上有一足够长的质量为m1的平板小车,正以速度v向右运动,现将以质量为m2的木块无初速度地放上小车,由于木块和小车间的摩擦力的作用,小车的速度将发生变化,为使小车保持原来的运动速度不变,必须及时对小车施加一向右的水平恒力,当该力作用一段时间后把它撤去时,木块恰能随小车一起以速度v共同向右运动,设木块和小车间的动摩擦因数为μ,求这个过程中: