题目内容
【题目】如图所示,在xOy直角坐标系中,第一象限内的等腰直角三角形ABO区域内有水平向左的匀强电场(电场强度大小未知),在第二象限边长为L的正方形CBOM区域内有竖直向下的匀强电场,电场强度大小为E0,现有一带正电粒子(重力不计)从AB边上的A点由静止释放,恰好能通过M点.
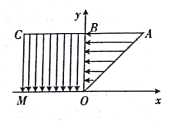
(1)求ABO区域内的匀强电场的电场强度大小E1;
(2)若ABO区域内的匀强电场的电场强度为3E0,要使从AO线上某点由静止释放题述相同的带电粒子,通过坐标为(-2L,0)的点,求释放点的坐标.
【答案】(1)![]() (2)坐标为(
(2)坐标为(![]() ,
,![]() )
)
【解析】试题分析:(1)先应用动能定理求出粒子射出第一象限的速度大小,再利用类平抛运动规律求解电场;
(2)综合动能定理和类平抛运动规律求解坐标。
(1) 设粒子的质量为m,电荷量为q.射出第一象限时的速度大小为v.在第一象限的电场中加速时,根据动能定理有,
![]()
要使粒子过M点.在第二象限电场中偏转时,竖直方向和水平方向的位移大小均为L
![]() ,解得:
,解得:![]() ;
;
(2) 设从OA上坐标为(x,y)出发的带电粒子.通过第一象限电场过程中.出电场时速度为v1.其在第一象限电场中加速时.根据动能定理有:
![]()
要使粒子过坐标为(-2L,0)点.在第二象限电场中偏转时,竖直方向位移为y1,水平方向位移为L,则![]()
转电粒子运动轨迹如图所示
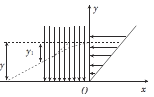
由图可知:得:![]()
得:![]()
其中y=x
解得:![]()
即释放点坐标为![]() 。
。

练习册系列答案
相关题目