Question

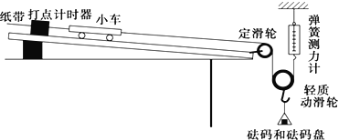
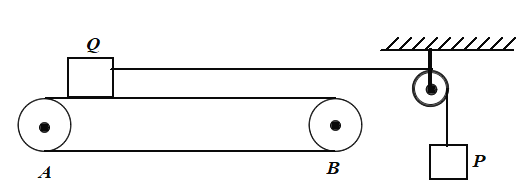
【题目】如图所示，水平传送带AB间的距离为16m，质量分别为2kg、4kg的物块P、Q，通过绕在光滑定滑轮上的细线连接，Q在传送带的左端且连接物块Q的细线水平，当传送带以8m/s的速度逆时针转动时，Q恰好静止。取重力加速度g=10m/s2，最大静摩擦力等于滑动摩擦力。当传送带以8m/s的速度顺时针转动时，下列说法正确的是（ ）

A.Q与传送带间的动摩擦因数为0.5

B.Q从传送带左端滑到右端所用的时间为2.4s

C.整个过程中，Q相对传送带运动的距离为4.8m

D.Q从传送带左端滑到右端的过程细线受到的拉力为20N

Answer 1

【答案】AC

【解析】

A．当传送带以v=8m/s逆时针转动时，Q恰好静止不动，对Q受力分析，则有

即

代入数据解得，故A正确；

B．当传送带突然以v=8m/s顺时针转动，物体Q做初速度为零的匀加速直线运动，根据牛顿第二定律有

解得m/s2，当速度达到传送带速度即8m/s后，做匀速直线运动，根据速度时间公式有

代入数据解得匀加速的时间为s，匀加速的位移为

代入数据解得x=4.8m，则匀速运动的时间为

代入数据解得s，Q从传送带左端滑到右端所用的时间为

s

故B错误；

C．加速阶段的位移之差为

m

而匀速阶段Q相对传送带静止，没有相对位移，故整个过程中，Q相对传送带运动的距离为4.8m，故C正确；

D．当Q加速时，对P分析，根据牛顿第二定律有

代入数据解得N；

之后做匀速直线运动，对对P分析，根据平衡条件有

N

故D错误。

故选AC。