题目内容
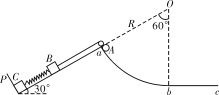
【题目】如图所示,直角三角形的斜边倾角∠C=30°,底边BC长为2L、处在水平位置,斜边AC是光滑绝缘的,在底边中点O处固定一正点电荷,一个质量为m、电量为q的带负电的质点从斜面顶端A沿斜边滑下.滑到斜边上的垂足D时速度为v。则
A. 质点的运动是先匀加速后匀减速运动
B. 质点在运动中动能与电勢能之和不发生变化
C. 质点运动到非常近斜边底端C点时的速度为![]()
D. 质点运动到非常挨近斜边底端C点时的加速度为g/2
【答案】C
【解析】
在直角三角形底边中点O处放置一正电荷Q,设OC=OD,则知C、D的电势相等;列出等式求出接近斜边底端C点时动能,对质点在D、C点进行受力分析,运用正交分解和牛顿第二定律列出等式求解C点的加速度和速度.
A.质点运动过程中,电场力的大小和方向是变化的,故合力的大小是变化的,故加速度也是变化的,故质点的运动不可能是匀变速运动,选项A错误;
B.小球受重力、支持力和电场力,支持力不做功,重力做功等于重力势能的减小量,电场力做功等于电势能的减小量,故在质点的运动中动能、电势能、重力势能三者之和守恒,因质点的重力势能减小,则质点在运动中动能与电势能之和增加,选项B错误;
C. DC两点的电势相等,则对从D到C过程,电场力做功为零,根据动能定理,有:mgLsin60°=![]() mvC2
mvC2![]() mv2,解得:
mv2,解得:![]() ,故C正确;
,故C正确;
D.质点滑到C点时,受重力、电场力、支持力,由牛顿第二定律得:mgsin30°-Fcos30°=maC,其中:![]() ,联立两式解得:
,联立两式解得:![]() ,方向平行于斜面向下。故D错误;
,方向平行于斜面向下。故D错误;
故选C。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目