题目内容
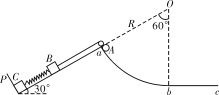
【题目】如图所示，在倾角为30°的光滑斜面上，一轻质弹簧两端连接两个质量均为m＝1 kg的物块B和C。物块C紧靠着挡板P，物块B通过一跨过光滑定滑轮的轻质细绳与质量m0＝8 kg、可视为质点的小球A相连，与物块B相连的细绳平行于斜面，小球A在外力作用下静止在对应圆心角为60°、半径R＝2 m的光滑圆弧轨道的最高点a处，此时细绳恰好伸直且无拉力，圆弧轨道的最低点b与光滑水平轨道bc相切。现由静止释放小球A，当小球A滑至b点时，物块B未到达a点，物块C恰好离开挡板P，此时细绳断裂。已知重力加速度g取10 m/s2，弹簧始终处于弹性限度内，细绳不可伸长，定滑轮的大小不计。求：
(1)弹簧的劲度系数；
(2)在细绳断裂后的瞬间，小球A对圆弧轨道的压力大小。
【答案】（1）5 N/m （2）144 N
【解析】
(1)小球A位于a处时，绳无张力且物块B静止，故弹簧处于压缩状态
对B由平衡条件有kx＝mgsin 30°
当C恰好离开挡板P时，C的加速度为0，故弹簧处于拉升状态
对C由平衡条件有kx′＝mgsin 30°
由几何关系知R＝x＋x′
代入数据解得k＝
＝5 N/m
(2)物块A在a处与在b处时，弹簧的形变量相同，弹性势能相同，故A在a处与在b处时，A、B系统的机械能相等，有m0gR(1－cos 60°)＝mgRsin 30°＋
m0vA2＋mvB2
将A在b处的速度分解，由速度分解关系有vAcos 30°＝vB
代入数据解得vA＝
＝4 m/s
在b处，对A由牛顿定律有N－m0g＝m0
代入数据解得N＝m0g＋m0＝144 N
由牛顿第三定律，小球A对圆轨道的压力大小为N′＝144 N
练习册系列答案
相关题目
