题目内容
 一质量为3m的平板小车C放在光滑的水平面上,它的上表面粗糙、很长、沿着水平方向.现有质量分别为m、2m的两个小物体A和B,各以相同大小的v0从小车左、右两端迎面滑上小车(如图所示),若A、B与小车上表面间的动摩擦因数均是μ,求:
一质量为3m的平板小车C放在光滑的水平面上,它的上表面粗糙、很长、沿着水平方向.现有质量分别为m、2m的两个小物体A和B,各以相同大小的v0从小车左、右两端迎面滑上小车(如图所示),若A、B与小车上表面间的动摩擦因数均是μ,求:(1)到A的速度减为零时,小车C速度的大小和方向;
(2)从A、B滑上小车起到A、B、C达到相对静止,一共经历了多长的时间.
分析:(1)由于B对C的摩擦力大于A对C的摩擦力,因此,A、B滑上小车后,小车C向左做加速运动,A向右做匀减速运动,B向左做匀减速运动,B与C先达到相对静止(此时A仍向右运动),A的速度为零后,会向左做加速运动,最终和A、B达到共同速度,一起做匀速运动.三个物体组成的系统合外力为零,动量守恒.当A的速度减为零时,B、C的速度相等,根据动量守恒列式求解小车C速度的大小和方向;
(2)当A、B都停止运动时,系统动量守恒,根据动量守恒求出A、B在车上都停止滑动时车的速度,抓住当A与小车速度相同时,A与车之间将不会相对滑动了,对B研究,由动量定理或结合牛顿第二定律和运动学公式求出B再与小车相对静止所需的时间,从而得出总时间.
(2)当A、B都停止运动时,系统动量守恒,根据动量守恒求出A、B在车上都停止滑动时车的速度,抓住当A与小车速度相同时,A与车之间将不会相对滑动了,对B研究,由动量定理或结合牛顿第二定律和运动学公式求出B再与小车相对静止所需的时间,从而得出总时间.
解答:解:(1)当A的速度减为零时,B、C的速度相等,根据A、B、C组成的系统在水平方向动量守恒:
2mv0-mv0=(2m+3m)vC①
得:vC=
v0,方向向左 ②
(2)设A、B、C三物体,达到相对静止时,它们的速度为v,根据A、B、C组成的系统在水平方向动量守恒:
2mv0-mv0=(m+2m+3m)v ③
得v=
v0 ④
对A物体的运动的整个过程用动量定理,μmgt=mv-mv0 ⑤
得:t=
⑥
答:
(1)到A的速度减为零时,小车C速度的大小为
v0,方向向左.
(2)从A、B滑上小车起到A、B、C达到相对静止,一共经历了
的时间.
2mv0-mv0=(2m+3m)vC①
得:vC=
| 1 |
| 5 |
(2)设A、B、C三物体,达到相对静止时,它们的速度为v,根据A、B、C组成的系统在水平方向动量守恒:
2mv0-mv0=(m+2m+3m)v ③
得v=
| 1 |
| 6 |
对A物体的运动的整个过程用动量定理,μmgt=mv-mv0 ⑤
得:t=
| 7v0 |
| 6μg |
答:
(1)到A的速度减为零时,小车C速度的大小为
| 1 |
| 5 |
(2)从A、B滑上小车起到A、B、C达到相对静止,一共经历了
| 7v0 |
| 6μg |
点评:本题综合考查了牛顿第二定律、动量守恒定律和运动学公式,因为要求出运动的时间,所以必须理清A、B以及小车在整个过程中的运动情况,由动量定理或结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
 (2008?卢湾区模拟)如图所示,一块质量为0.6kg均匀平板AB长0.8m,其左端搁在水平地面上,板与地面的夹角为370,板中心C垂直固定在轻支架上,支架长OC为0.3m,支架下端与水平固定转轴O连接.在平板A点处有一质量为0.5kg的小物体m以初速v0沿板向上运动,物体与平板间的动摩擦因数为0.2,g取10m/s2.试求:
(2008?卢湾区模拟)如图所示,一块质量为0.6kg均匀平板AB长0.8m,其左端搁在水平地面上,板与地面的夹角为370,板中心C垂直固定在轻支架上,支架长OC为0.3m,支架下端与水平固定转轴O连接.在平板A点处有一质量为0.5kg的小物体m以初速v0沿板向上运动,物体与平板间的动摩擦因数为0.2,g取10m/s2.试求: 2.小物体运动到距B端多远恰能使平板翻转?
2.小物体运动到距B端多远恰能使平板翻转? 【小题2】小物体运动到距B端多远恰能使平板翻转?
【小题2】小物体运动到距B端多远恰能使平板翻转?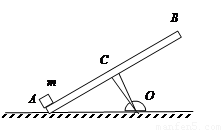 2.小物体运动到距B端多远恰能使平板翻转?
2.小物体运动到距B端多远恰能使平板翻转?