题目内容
2.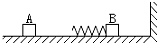 如图所示,在光滑的水平面上,质量为2m物体A以初速度v0向右开始运动,质量为m的物体B静置在光滑水平面上,其左侧连接一轻质弹簧;当物体A压缩轻质弹簧至物体A?B刚好相对静止时,物体B碰在右侧竖直墙上,并与墙粘合?求:
如图所示,在光滑的水平面上,质量为2m物体A以初速度v0向右开始运动,质量为m的物体B静置在光滑水平面上,其左侧连接一轻质弹簧;当物体A压缩轻质弹簧至物体A?B刚好相对静止时,物体B碰在右侧竖直墙上,并与墙粘合?求:(ⅰ)轻质弹簧在整个过程中具有的最大弹性势能;
(ⅱ)物体A在全过程中,弹簧弹力对A的冲量大小?
分析 (1)系统动量守恒,由动量守恒定律与机械能守恒定律可以求出弹性势能.
(2)由机械能守恒求得速度,再由动量定理可求得弹簧弹力对A的冲量大小.
解答 解:(1)当A球与弹簧接触以后,在弹力作用下减速运动,而B球在弹力作用下加速运动,
弹簧势能增加,当A、B速度相同时,弹簧的势能最大.
设A、B的共同速度为v,弹簧的最大势能为Ep,
A、B系统动量守恒,以向右为正方向,由动量守恒定律得:
m1v0=(m1+m2)v,
由机械能守恒定律的:$\frac{1}{2}$m1v02=$\frac{1}{2}$(m1+m2)v2+Ep,
联立两式解得:Ep=$\frac{{m}_{2}{v}_{0}^{2}}{{m}_{1}+{m}_{2}}$=$\frac{m{v}_{0}^{2}}{3}$
物体A压缩弹簧至运动到最右端时,其动能全部转化为弹簧的弹性势能,则弹簧具有的最大弹性势能为EP2=EP+$\frac{1}{2}$mv12=$\frac{7m{v}_{0}^{2}}{9}$;
(2)最后物体A离开弹簧时,设其速度大小为v3,弹簧的弹性势能全部转化为物体A的动能,则
EP2=$\frac{1}{2}$•2mv22
可解得:v2=$\frac{\sqrt{7}{v}_{0}}{3}$
规定向左为正方向,对A应用动量定理I=2mv2-(-2mv0)
可解得I=$\frac{6+2\sqrt{7}}{3}$mv0
答:(1)整个过程中弹簧弹性势能最大值是为$\frac{7m{v}_{0}^{2}}{9}$;
(2)物体A在全过程中,弹簧弹力对A的冲量大小为$\frac{6+2\sqrt{7}}{3}$mv0
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与机械能守恒定律即可正确解题.

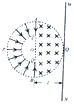
 伽利略研究自由落体运动时,让小球从倾角较小的光滑斜面滑下,然后在不同的倾角条件下进行多次实验,实验示意图如图所示.则下列说法错误的是( )
伽利略研究自由落体运动时,让小球从倾角较小的光滑斜面滑下,然后在不同的倾角条件下进行多次实验,实验示意图如图所示.则下列说法错误的是( )| A. | 斜面小角度是为了延长小球在斜面上运动的时间 | |
| B. | 实验结果说明小球在斜面上速度随时间均匀增加 | |
| C. | 实验结果说明小球在斜面上运动的距离随时间均匀增加 | |
| D. | 通过实验和逻辑推理,伽利略得出自由落体运动时一种匀加速直线运动 |
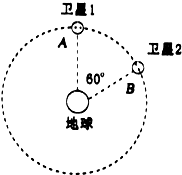 北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )| A. | 这两颗卫星的加速度大小相等,均为$\frac{Rg}{r}$ | |
| B. | 这两颗卫星的线速度大小相等,均为$\sqrt{gr}$ | |
| C. | 卫星1向后喷气就一定能追上卫星2 | |
| D. | 卫星1由位置A运动到位置B所需的时间为$\frac{πr}{3Rg}$$\sqrt{gr}$ |
 如图所示,足够长金属导轨竖直放置,金属棒ab、cd均通过棒两端的环套在金属导轨上并与导轨保持良好的接触?虚线上方有垂直纸面向里的匀强磁场,虚线下方有竖直向下的匀强磁场.ab、cd棒与导轨间动摩擦因数均为μ,两棒总电阻为R,导轨电阻不计.开始两棒均静止在图示位置,当cd棒无初速释放,同时对ab棒施加竖直向上的拉力F,沿导轨向上做匀加速运动.则( )
如图所示,足够长金属导轨竖直放置,金属棒ab、cd均通过棒两端的环套在金属导轨上并与导轨保持良好的接触?虚线上方有垂直纸面向里的匀强磁场,虚线下方有竖直向下的匀强磁场.ab、cd棒与导轨间动摩擦因数均为μ,两棒总电阻为R,导轨电阻不计.开始两棒均静止在图示位置,当cd棒无初速释放,同时对ab棒施加竖直向上的拉力F,沿导轨向上做匀加速运动.则( )| A. | ab棒中的电流方向由b到a | |
| B. | 拉力F的功率不断增大 | |
| C. | cd棒先加速运动后匀速运动 | |
| D. | 力F做的功等于两金属棒产生的电热与增加的机械能之和 |
| A. | 单摆运动时,摆球要受到大小不变的向心力 | |
| B. | 单摆运动时,摆球所受到的重力沿切向分力为回复力 | |
| C. | 单摆运动到平衡位置时,所受到的回复力为零 | |
| D. | 单摆运动到平衡位置时,所受到的合力为零 |
| A. | 若其质量加倍,则轨道半径也要加倍 | |
| B. | 它在北京上空运行,故可用于我国的电视广播 | |
| C. | 它以第一宇宙速度运行 | |
| D. | 它运行的角速度与地球自转角速度相同 |
 “太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行于边界ACDB,0点到MN板的距离OQ为Lo在边界ACDB和收集板MN之间有一以0为圆心、L为半径的半圆形匀强磁场.方向垂直纸面向里.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不汁粒子间的相互作用和其它星球对粒子引力的影响.
“太空粒子探测器”由加速、偏转和收集三部分装置组成,其原理如图所示:辐射状的加速电场区域边界为两个同心半圆弧$\widehat{AB}$和$\widehat{CD}$,圆心为O,弧$\widehat{AB}$的半径为L,P为弧$\widehat{AB}$的中点,两圆弧间的电势差大小为U.足够长的收集板MN平行于边界ACDB,0点到MN板的距离OQ为Lo在边界ACDB和收集板MN之间有一以0为圆心、L为半径的半圆形匀强磁场.方向垂直纸面向里.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到弧$\widehat{APB}$上,并被加速电场从静止开始加速,不汁粒子间的相互作用和其它星球对粒子引力的影响. 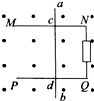 如图所示,在一磁感应强度B=0.5T的匀强磁场中,垂直于磁场方向水平放置着两根相距L=0.1m的平行金属导轨MN和PQ,导轨的电阻忽略不计,在两根导轨的端点N,Q之间连接一阻值为R=0.3Ω的电阻.导轨上跨放着一根R0=0.2Ω的金属棒ab,当金属棒以速度v=4.0m/s向左匀速运动时.试求:
如图所示,在一磁感应强度B=0.5T的匀强磁场中,垂直于磁场方向水平放置着两根相距L=0.1m的平行金属导轨MN和PQ,导轨的电阻忽略不计,在两根导轨的端点N,Q之间连接一阻值为R=0.3Ω的电阻.导轨上跨放着一根R0=0.2Ω的金属棒ab,当金属棒以速度v=4.0m/s向左匀速运动时.试求: 如图所示,用50N的力拉一个质量为10kg的物体在水平地面上前进,若物体前进了10m,拉力F做的功W1=400J,如果物体与水平面间动摩擦因数μ=0.1,物体克服阻力做功W3=70J.外力对物体所做的总功为330焦.
如图所示,用50N的力拉一个质量为10kg的物体在水平地面上前进,若物体前进了10m,拉力F做的功W1=400J,如果物体与水平面间动摩擦因数μ=0.1,物体克服阻力做功W3=70J.外力对物体所做的总功为330焦.