题目内容
1.平抛一物体,当抛出2s后,它的速度方向与水平方向成45°角,落地时速度方向与水平方向成60°角,取g=10m/s2.(1)落地速度;
(2)开始抛出时距地面的高度.
分析 (1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.将两秒后的速度进行分解,根据vy=gt求出竖直方向上的分速度,再根据角度关系求出平抛运动的初速度.将落地的速度进行分解,水平方向上的速度不变,根据水平初速度求出落地时的速度.
(2)根据落地时的速度求出竖直方向上的分速度,再根据${{v}_{y}}^{2}=2gh$求出抛出点距地面的高度
解答 解:(1)2s后竖直方向上的分速度vy1=gt=20m/s
$tan45°=\frac{{v}_{y}}{{v}_{x}}=1$,则v0=vx=vy=20m/s.
故物体抛出时的初速度为20m/s.
落地时速度方向与水平成60°角.
所以$cos60°=\frac{{v}_{0}}{v}$,则v=$\frac{{v}_{0}}{cos60°}=\frac{20}{\frac{1}{2}}m/s=40m/s$.
故落地时的速度为40m/s.
(2)落地时竖直方向的分速度${v}_{y}=vsin60°=20\sqrt{3}m/s$
根据${{v}_{y}}^{2}=2gh$得,h=$\frac{{{v}_{y}}^{2}}{2g}=\frac{1200}{20}m=60m$
故抛出点距离地面的高度为60m.
答:(1)落地速度是40m/s;
(2)开始抛出时距地面的高度是60m.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
11.下列有关光现象的说法中正确的是 ( )
| A. | 早晨看到的从东方升起的太阳是由全反射形成的太阳的像 | |
| B. | 光的衍射现象会使我们看到刮胡须的刀片的影子边缘模糊不清 | |
| C. | 光的折射现象会使我们看到水中物体的“视深”比实际深度浅 | |
| D. | 海市蜃楼是光的干涉的结果 | |
| E. | 光导纤维利用光的全反射传递信息 |
12.在排球比赛中如果运动员在近网处沿水平方向扣球.若把扣后排球的运动近似看作质点的平抛运动,则下列四种情况中,排球最有可能出界的是( )
| A. | 扣球点较低,扣出时排球的速度较大 | |
| B. | 扣球点较低,扣出时排球的速度较小 | |
| C. | 扣球点较高,扣出时排球的速度较大 | |
| D. | 扣球点较高,扣出时排球的速度较小 |
9. 2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )
2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )
 2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )
2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )| A. | 楼在倾倒 | B. | 人在运动 | ||
| C. | 选择了旁边更高的楼为参考系 | D. | 选择了高空运动的云为参考系 |
2.如图所示的电场中,下列关于A点和B点相比较的说法中正确的是( )
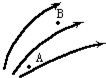

| A. | EA=EB | B. | UA<UB | C. | EA<EB | D. | UA>UB |
7.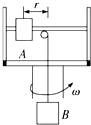 如图所示,质量为M的物体A穿在离心机的水平光滑杆上,A用绳子与另一质量为m的物体B相连.当离心机以角速度ω绕竖直轴旋转时,A离转轴轴心的距离是R;当ω增大到原来的2倍时,调整A离转轴的距离,使之达到新的稳定状态.则( )
如图所示,质量为M的物体A穿在离心机的水平光滑杆上,A用绳子与另一质量为m的物体B相连.当离心机以角速度ω绕竖直轴旋转时,A离转轴轴心的距离是R;当ω增大到原来的2倍时,调整A离转轴的距离,使之达到新的稳定状态.则( )
 如图所示,质量为M的物体A穿在离心机的水平光滑杆上,A用绳子与另一质量为m的物体B相连.当离心机以角速度ω绕竖直轴旋转时,A离转轴轴心的距离是R;当ω增大到原来的2倍时,调整A离转轴的距离,使之达到新的稳定状态.则( )
如图所示,质量为M的物体A穿在离心机的水平光滑杆上,A用绳子与另一质量为m的物体B相连.当离心机以角速度ω绕竖直轴旋转时,A离转轴轴心的距离是R;当ω增大到原来的2倍时,调整A离转轴的距离,使之达到新的稳定状态.则( )| A. | 物体A受到的向心力增大 | B. | 物体A的线速度大小不变 | ||
| C. | 物体A离转轴的距离是$\frac{r}{2}$ | D. | 物体A离转轴的距离是$\frac{r}{4}$ |
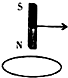 如图所示,水平放置的绝对绝缘桌面上有一个金属圆环,圆心的正上方有一个竖直的条形磁铁,当条形磁铁水平向右移动时,金属圆环受到驱动力的方向是( )
如图所示,水平放置的绝对绝缘桌面上有一个金属圆环,圆心的正上方有一个竖直的条形磁铁,当条形磁铁水平向右移动时,金属圆环受到驱动力的方向是( )