题目内容
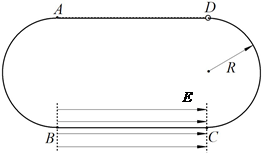
(12分)如图所示,宇航员从空间站C(绕地球运行)上释放了一颗质量m的探测卫星P 。该卫星通过一条柔软的细轻绳与空间站连接,稳定时卫星始终在空间站的正下方,到空间站的距离为l 。已知空间站的轨道为圆形,周期为T,地球半径为R,地球同步卫星到地面的高度为H0,地球自转周期为T0,万有引力常量为G,忽略卫星拉力对空间站轨道的影响,求:
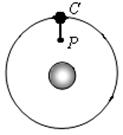
(1)空间站离地面的高度H及卫星离地面的高度h;
(2)卫星所受轻绳拉力的大小。

(1)空间站离地面的高度H及卫星离地面的高度h;
(2)卫星所受轻绳拉力的大小。
(1)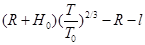 ;(2)
;(2)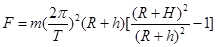
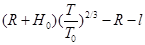 ;(2)
;(2)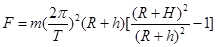
试题分析:(1)设空间站离地面的高度为H, 因为同步卫星的周期和地球自转周期相同,根据开普勒第三定律以及题意有:
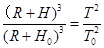 ① ( 2分)
① ( 2分)即:
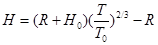 ② ( 2分)
② ( 2分)卫星的高度: h =
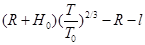 ③ ( 2分)
③ ( 2分)(2)卫星在细绳的拉力 F 和地球引力作用下跟随空间站一起绕地球作周期为 T 的圆周运动,有:
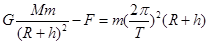 ④ ( 2分)
④ ( 2分)式中 M为地球质量.空间站在地球引力作用下绕地球作周期为 T 的圆周运动
故有:
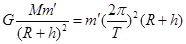 ⑤ ( 2分)
⑤ ( 2分)式中m’为空间站的质量.由④、⑤两式得:
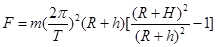 ⑥ ( 2分)
⑥ ( 2分)
练习册系列答案
相关题目
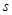 ,则下列运算公式中不正确的是( )
,则下列运算公式中不正确的是( )
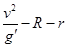
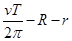
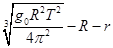
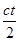


 FT
FT