题目内容
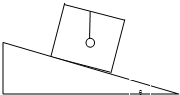
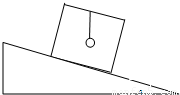
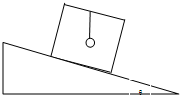 如图所示,木箱的顶上悬挂一小球,当木箱从倾角为θ的斜面上自由滑下,木箱内悬挂小球的细线呈竖直方向,设小球的质量为m,木箱的质量为M,那么当木箱从斜面底端以某一初速度沿斜面向上滑行达到稳定时,求细线对小球拉力的大小为
如图所示,木箱的顶上悬挂一小球,当木箱从倾角为θ的斜面上自由滑下,木箱内悬挂小球的细线呈竖直方向,设小球的质量为m,木箱的质量为M,那么当木箱从斜面底端以某一初速度沿斜面向上滑行达到稳定时,求细线对小球拉力的大小为mg
mg
.分析:木箱自由滑下时,细线无倾斜,说明木箱为匀速下滑,根据平衡条件求出滑动摩擦力,当木箱向斜面上滑时根据牛顿第二定律求出加速度,再对小球进行受力分析即可求解.
解答:解:木箱自由滑下时,细线无倾斜,说明木箱为匀速下滑,有:f=μ(M+m)gcosθ=(M+m)gsinθ
当木箱向斜面上滑时有:
(M+m)a=(M+m)gsinθ+f=2(M+m)gsinθ
解得:a=2gsinθ
对小球根据几何关系有:
T2=m2g2+m2a2-2mg?masinθ=m2g2
所以:T=mg
故答案为:mg
当木箱向斜面上滑时有:
(M+m)a=(M+m)gsinθ+f=2(M+m)gsinθ
解得:a=2gsinθ
对小球根据几何关系有:
T2=m2g2+m2a2-2mg?masinθ=m2g2
所以:T=mg
故答案为:mg
点评:本题的关键是对木箱和小球的受力分析,根据牛顿第二定律结合整体法和隔离法的应用求解,难度适中.

练习册系列答案
相关题目

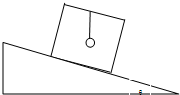 如图所示,木箱的顶上悬挂一小球,当木箱从倾角为θ的斜面上自由滑下,木箱内悬挂小球的细线呈竖直方向,设小球的质量为m,木箱的质量为M,那么当木箱从斜面底端以某一初速度沿斜面向上滑行达到稳定时,求细线对小球拉力的大小为________.
如图所示,木箱的顶上悬挂一小球,当木箱从倾角为θ的斜面上自由滑下,木箱内悬挂小球的细线呈竖直方向,设小球的质量为m,木箱的质量为M,那么当木箱从斜面底端以某一初速度沿斜面向上滑行达到稳定时,求细线对小球拉力的大小为________.