题目内容
12.已知质量分布均匀的球壳对对壳内的物体的引力为0.假设地球是一半径为R的质量分布均匀的球体,地球表面的重力加速度大小为g.试求:( 1 )在地面上方离地面距离为$\frac{R}{2}$处的重力加速度大小与在地面下方地球内部离地面距离为$\frac{R}{2}$处的重力加速度大小之比为多少?
( 2 )设想地球的密度不变,自转周期不变,但地球球体半径变为原来的一半,仅考虑地球和同步卫星之间的相互作用力,则该“设想地球”的同步卫星的轨道半径与以前地球的同步卫星轨道半径的比值是多少?
分析 (1)根据题意知,地球表面的重力加速度等于半径为R的球体在表面产生的加速度,在其内部距离地心距离为r处一点的加速度相当于半径为r的球体在其表面产生的加速度,根据万有引力提供向心力求解;
(2)地球和同步卫星的万有引力提供同步卫星转动的向心力,根据万有引力提供向心力公式列式,联立方程求解.
解答 解:(1)根据万有引力提供向心力得:
$G\frac{{M}_{g1}m}{(R+0.5R)^{2}}=m{g}_{1}$,
$G\frac{{M}_{g2}m}{{(R-0.5R)}^{2}}=m{g}_{2}$,
且有:$\frac{{M}_{g1}}{{M}_{g2}}=\frac{ρ•\frac{4}{3}π{R}^{3}}{ρ•\frac{4}{3}π(\frac{R}{2})^{2}}=\frac{8}{1}$,
则得:$\frac{{g}_{1}}{{g}_{2}}=\frac{8}{1}×\frac{1}{9}=\frac{8}{9}$
(2)地球和同步卫星的万有引力提供同步卫星转动的向心力,则有:
$G\frac{{M}_{g1}m}{{{r}_{1}}^{2}}=m\frac{4{π}^{2}{r}_{1}}{{T}^{2}}$,
$G\frac{{M}_{g2}m}{{{r}_{2}}^{2}}=m\frac{4{π}^{2}{r}_{2}}{{T}^{2}}$,
而${M}_{g1}=ρ•\frac{4}{3}π{R}^{2}$,${M}_{g2}=ρ•\frac{4}{3}π({\frac{R}{2})}^{2}$,
解得:$\frac{{r}_{2}}{{r}_{1}}=\frac{1}{2}$
答:( 1 )在地面上方离地面距离为$\frac{R}{2}$处的重力加速度大小与在地面下方地球内部离地面距离为$\frac{R}{2}$处的重力加速度大小之比为8:9;
( 2 )设想地球的密度不变,自转周期不变,但地球球体半径变为原来的一半,仅考虑地球和同步卫星之间的相互作用力,则该“设想地球”的同步卫星的轨道半径与以前地球的同步卫星轨道半径的比值是1:2.
点评 本题主要考查了万有引力提供向心力公式的直接应用,知道质量与半径之间的关系,明确地球的密度是不变的,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,光滑水平面上两小球发生弹性正碰,从两球接触至分离的过程中,对两个小球组成的系统,下列说法正确的是( )
如图所示,光滑水平面上两小球发生弹性正碰,从两球接触至分离的过程中,对两个小球组成的系统,下列说法正确的是( )| A. | 弹性势能增加 | B. | 动量守恒 | C. | 动能守恒 | D. | 机械能守恒 |
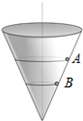 如图所示,一个内壁光滑的圆锥筒,其轴线垂直于水平面,圆锥筒固定在水平地面不动.有两个质量均为m的小球A和小球B紧贴着筒内壁在水平面内做匀速圆周运动,小球B所在的高度为小球A所在的高度一半.下列说法正确的是( )
如图所示,一个内壁光滑的圆锥筒,其轴线垂直于水平面,圆锥筒固定在水平地面不动.有两个质量均为m的小球A和小球B紧贴着筒内壁在水平面内做匀速圆周运动,小球B所在的高度为小球A所在的高度一半.下列说法正确的是( )| A. | 小球A、B所受的支持力大小之比为2:1 | |
| B. | 小球A、B的加速度的大小之比为1:1 | |
| C. | 小球A、B的角速度之比为$\sqrt{2}$:1 | |
| D. | 小球A、B的线速度之比为$\sqrt{2}$:1 |
 一质点沿某一条直线运动时的速度-时间图象如图所示,则以下说法中正确的是( )
一质点沿某一条直线运动时的速度-时间图象如图所示,则以下说法中正确的是( )| A. | 第1s末质点的位移和速度都改变方向 | |
| B. | 第2s末质点的加速度为0 | |
| C. | 第4s末质点的位移为零 | |
| D. | 第2s末质点的位移最大 |
| A. | 法拉第预言了电磁波的存在 | |
| B. | 电磁波在介质中的传播速度为3×108m/s | |
| C. | 光波是电磁波 | |
| D. | 电磁波在真空中的频率越大,传播速度越大 |
| A. | 质量大的物体不能看成质点,质量小的物体可以看成质点 | |
| B. | 物体在5s内指的是物体在4s末到5s末这1s的时间 | |
| C. | 质点做单向的直线运动时,位移等于路程 | |
| D. | 经过提速后列车的速度达到159km/h,此速度应指平均速度 |
 有一个额定电压为2.8V,功率约为0.8W的小灯泡,现要描绘这个灯泡的I-U图线,有下列器材供选用:
有一个额定电压为2.8V,功率约为0.8W的小灯泡,现要描绘这个灯泡的I-U图线,有下列器材供选用: 如图所示,置于水平地面上的相同材料的质量分别为m=2kg和m0=3kg的两物体用细绳连接,在m0上施加一水平恒力F=20N,使两物体做匀加速直线运动,
如图所示,置于水平地面上的相同材料的质量分别为m=2kg和m0=3kg的两物体用细绳连接,在m0上施加一水平恒力F=20N,使两物体做匀加速直线运动,