题目内容
3.小球做匀速圆周运动,半径为R,向心加速率为a,则( )| A. | 小球受到的合力是一个恒力 | B. | 小球运动的角速度为$\sqrt{\frac{a}{R}}$ | ||
| C. | 小球在时间t内通过的位移为$\sqrt{aR}t$ | D. | 小球的运动周期为2π$\sqrt{\frac{R}{a}}$ |
分析 小球做匀速圆周运动,靠合力提供向心力,合力是变力.根据向心加速度与线速度、角速度的关系求出线速度和角速度的大小,从而求出周期的大小.
解答 解:A、小球做匀速圆周运动,合力提供向心力,合力的方向始终指向圆心,方向时刻改变,故A错误.
B、根据a=Rω2得,小球运动的角速度$ω=\sqrt{\frac{a}{R}}$,故B正确.
C、根据$a=\frac{{v}^{2}}{R}$得,小球的线速度v=$\sqrt{aR}$,则小球通过的弧长s=$vt=\sqrt{aR}t$,与位移的大小不等,故C错误.
D、小球运动的周期T=$\frac{2π}{ω}=2π\sqrt{\frac{R}{a}}$,故D正确.
故选:BD.
点评 解决本题的关键知道线速度、角速度、周期、向心加速度之间的关系,并能灵活运用,基础题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
13.2013年12月2日1时30分,“嫦娥三号”探测器由长征三号乙运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察.在接近月球时,嫦娥三号要利用自身的火箭发动机点火减速,被月球引力俘获进入绕月轨道.这次减速只有一次机会,如果不能减速到一定程度,嫦娥三号将一去不回头离开月球和地球,漫游在更加遥远的深空;如果过分减速,嫦娥三号则可能直接撞击月球表面.则下列说法正确的是( )


| A. | 实施首次“刹车”的过程,将使得嫦娥三号损失的动能转化为势能,转化时机械能守恒 | |
| B. | 嫦娥三号被月球引力俘获后进入绕月轨道,并逐步由圆轨道变轨到椭圆轨道 | |
| C. | 嫦娥三号如果不能减速到一定程度,月球对它的引力将会做正功,将离开月球和地球 | |
| D. | 嫦娥三号如果过分减速,月球对它的引力将做正功,撞击月球表面时的速度将很大 |
11.质量相同的两个小球在光滑水平面上沿连心线同向运动,球1的动量为7kg•m/s,球2的动量为5kg•m/s,当球1追上球2时发生碰撞,则碰撞后两球动量变化的可能值是( )
| A. | △p1=-1 kg•m/s,△p2=1 kg•m/s | B. | △p1=-1 kg•m/s,△p2=4 kg•m/s | ||
| C. | △p1=-9 kg•m/s,△p2=9 kg•m/s | D. | △p1=-12 kg•m/s,△p2=10 kg•m/s |
18. 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )| A. | 电压有效值为220$\sqrt{2}$V | |
| B. | 电流的周期为0.01s | |
| C. | 如果在该电阻器两端并联一个交流电压表,该电压表的示数为220 V | |
| D. | 如果在该电路中串联一个交流电流表,该电流表的示数为2$\sqrt{2}$V |
8.如图所示的电路中,电源电动势为E,线圈L的电阻不计.以下判断正确的是( )


| A. | 闭合S,稳定后,电容器两端电压为E | |
| B. | 闭合S,稳定后,电容器的a极带正电 | |
| C. | 断开S的瞬间,电容器的a极板将带正电 | |
| D. | 闭合S的瞬间,电路中无电流 |
15.关于线圈在匀强磁场中转动产生的交变电流,下列说法中正确的是( )
| A. | 线圈每经过中性面一次,感应电流方向改变一次,感应电动势方向不变 | |
| B. | 线圈每转动一周,感应电流方向就改变一次 | |
| C. | 线圈平面每经过中性面一次,感应电流和感应电动势方向都要改变一次 | |
| D. | 线圈转动一周,感应电流和感应电动势方向都要改变一次 |
13.一列简谐横波,在t=0.6s时刻的图象如图甲所示,波上A质点的振动图象如图乙所示,则以下说法正确的是( )


| A. | 这列波沿x轴正方向传播,波速是$\frac{50}{3}$m/s | |
| B. | 从t=0.6s开始,紧接着的△t=0.6s时间内,A质点通过的路程是4m | |
| C. | 从t=0.6s开始,质点P比质点Q早0.4s到达波峰位置 | |
| D. | 从t=0.6s开始,再经0.15s质点Q第一次到达波谷位置 |
 根据不同的实验条件,进行了“探究平抛运动规律”的实验:
根据不同的实验条件,进行了“探究平抛运动规律”的实验: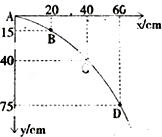 某同学在做研究平抛运动的试验时,忘记记下斜槽位置,如图所示中的A点为小球运动一段时间后的位置,他便以A为坐标原点,建立了水平方向和竖直方向的坐标轴,得到如图所示的图象,试根据图象求出:(g取10m/s2)
某同学在做研究平抛运动的试验时,忘记记下斜槽位置,如图所示中的A点为小球运动一段时间后的位置,他便以A为坐标原点,建立了水平方向和竖直方向的坐标轴,得到如图所示的图象,试根据图象求出:(g取10m/s2)