题目内容
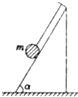如图所示，倾角α=53°的光滑斜面体上有一个小球m=1kg被平行于斜面的细绳系于斜面上，斜面体在水平面上沿直线运动，不计空气阻力，g=10m/s2，已知：sin53°=0.8，cos53°=0.6，则下列说法正确的是（ ）分析：（1）若斜面体匀速运动，小球也做匀速运动，根据平衡条件即可分析小球对斜面是否有压力；
（2）若绳子没有拉力，则小球只受重力和支持力，根据牛顿第二定律即可求出小球的加速度，跟题中的加速度进行比较，若小于题中加速度则有拉力，反之则没有拉力；
（3）若小球对斜面无压力，只小球只受重力和绳子的拉力，加速度方向水平向右，则斜面体的加速度也水平向右；
（3）小球和斜面具有相同的加速度，根据牛顿第二定律即可求出小球的合力，对小球进行受力分析即可求得绳子与竖直方向的夹角．
（2）若绳子没有拉力，则小球只受重力和支持力，根据牛顿第二定律即可求出小球的加速度，跟题中的加速度进行比较，若小于题中加速度则有拉力，反之则没有拉力；
（3）若小球对斜面无压力，只小球只受重力和绳子的拉力，加速度方向水平向右，则斜面体的加速度也水平向右；
（3）小球和斜面具有相同的加速度，根据牛顿第二定律即可求出小球的合力，对小球进行受力分析即可求得绳子与竖直方向的夹角．
解答：解：A、若斜面体匀速运动，小球也做匀速运动，则小球受力平衡，小球受重力和绳子的拉力及斜面对小球的支持力，这三个力合力为零，所以小球对斜面一定有压力，故A正确；
B、若绳子没有拉力，则小球只受重力和支持力，a=
=
=
m/s2＞12m/s2，所以绳子对小球肯定没有拉力，即小球对细绳也一定没有拉力，故B错误；
C、若小球对斜面无压力，只小球只受重力和绳子的拉力，加速度方向水平向右，则斜面体的加速度也水平向右，可以向右加速，也可以向左减速，故C错误；
D、当斜面对小球刚好没有支持力时，对小球进行受力分析，此时小球的加速度为：
=
=7.5m/s2＜10
m/s2则在此加速度下小球以脱离斜面体，
设此时细绳与竖直方向的夹角为θ，ma=mgtanθ，解得：tanθ=
，所以θ=60°，故D正确．
故选AD
B、若绳子没有拉力，则小球只受重力和支持力，a=
| F合 |
| m |
| mg |
| mtan37° |
| 40 |
| 3 |
C、若小球对斜面无压力，只小球只受重力和绳子的拉力，加速度方向水平向右，则斜面体的加速度也水平向右，可以向右加速，也可以向左减速，故C错误；
D、当斜面对小球刚好没有支持力时，对小球进行受力分析，此时小球的加速度为：
| F合 |
| m |
| mg |
| mtan53° |
| 3 |
设此时细绳与竖直方向的夹角为θ，ma=mgtanθ，解得：tanθ=
| 3 |
故选AD
点评：解答本题时要先求出绳子恰好没有拉力和斜面体对小球恰好没有支持力时的小球加速度，再跟题中所给的加速度进行比较以确定小球所处的状态，关键是对小球的受力分析，难度适中．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6m/s速度运动，运动方向如图所示．一个质量为m的物体（物体可以视为质点），从h=3.2m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其速率变化．物体与传送带间的动摩擦因数为0.5，物体向左最多能滑到传送带左右两端AB的中点处，重力加速度g=10m/s2，则：
（2011?双流县模拟）如图所示，倾角θ=30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T，范围足够大的匀强磁场中，磁场方向垂直于斜面向下．用平行于轨道的牵引力拉一根质量m=0.2kg、电阻R=1Ω放在导轨上的金属棒ab，使之由静止沿轨道向上运动，牵引力做功的功率恒为6W，当金属棒移动2.8m时，获得稳定速度，在此过程中金属棒产生的热量为5.8J，不计导轨电阻及一切摩擦，取g=10m/s2．求：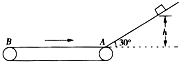
如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6m/s的速度运动，运动方向如图所示，物体与传送带间的动摩擦因数为0.5，A、B间的距离L=4.2m，g取10m/s2．如果将物体轻轻放在传送带左端的B点，它沿斜面上滑到最大高度需要多长时间？
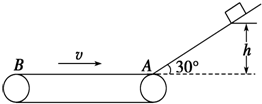如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6m/s的速度运动，运动方向如图所示．一个质量为2kg的物体（物体可以视为质点），从h=3.2m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失．物体与传送带间的动摩擦因数为0.5，g=10m/s2，则：
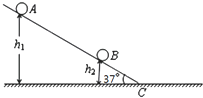如图所示，倾角为37°的足够长粗糙斜面下端与一足够长光滑水平面相接，斜面上有两小球A、B，距水平面高度分别为h1=5.4m和h2=0.6m．现由静止开始释放A球，经过一段时间t后，再由静止开始释放B球．A和B与斜面之间的动摩擦因素均为μ=0.5，重力加速度g=10m/s2，不计空气阻力，设小球经过斜面和水平面交界处C机械能不损失，（sin37°=0.6，cos37°=0.8）． 求：