题目内容
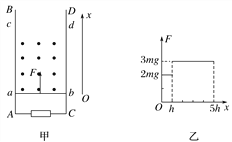
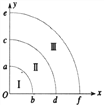
【题目】如图,坐标系xOy的第一象限内,以O为圆心半径分别为R、2R、3R的圆弧ab、cd、ef及两坐标轴围成I、II、III三个区域。I、II区域中存在磁感应强度大小为B0的匀强磁场,其中I区域的磁场方向垂直坐标平面向外、II区域的磁场方向垂直坐标平面向里。一质量为m、电荷量为q的带正电粒子,以某一初速度从坐标原点O沿+y方向射入磁场,与弧ab交点的坐标为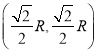 。求:
。求:
(1)粒子的初速度大小;
(2)粒子从O点运动到弧cd经历的时间t;
(3)若III区域中也存在垂直坐标平面的匀强磁场,为使粒子不能从弧ef上射出磁场,求磁感应强度B满足的条件。
【答案】(1) ![]() (2)
(2) ![]() (3)当B垂直向里时,
(3)当B垂直向里时, ![]() ;当B垂直向外时,
;当B垂直向外时, ![]()
【解析】试题分析:(1)根据几何关系求出半径,根据洛伦兹力提供向心力求解速度;(2)画出粒子运动轨迹过程图,利用所转过的弧长除以速度大小即可求出粒子运动时间;(3)由于磁场方向不确定,故存在两种情况,分情况讨论,当III区域的磁场方向垂直坐标平面向外和垂直坐标平面向里两种情况,找到临界条件,即轨迹与III区域的外边界相切,用洛伦兹力提供向心力与临界几何关系结合即可求出磁感应强度B的取值范围.
(1)如图所示
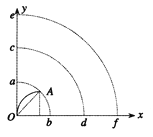
由几何关系知,粒子在区域I中运动时的半径为![]()
设粒子的初速度大小为v,由牛顿第二定律得: ![]()
联立解得: ![]()
(2)粒子在I区域的轨迹对应的圆心角为![]() ,故运动时间为
,故运动时间为![]() ,则有:
,则有: 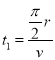
进入II区域后,粒子运动的偏转方向改变,但轨迹半径不变。轨迹与弧cd的交点C与A、O在一条直线上,运动轨迹如图所示
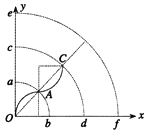
则粒子在I、II两区域的运动轨迹对应的圆心角相等,故运动时间相等
故粒子从O到C的运动时间为![]()
整理得: ![]()
(3)粒子经过C点时速度沿+y方向,由几何关系可知C点的坐标为![]()
若区域的磁场方向向里,粒子恰好从e点经过时,轨迹如图所示
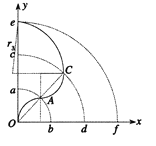
由几何关系知: ![]()
整理得: ![]()
则: ![]()
若III区域中的磁场方向向外,粒子的轨迹恰好与弧ef相切时,轨迹如图所示
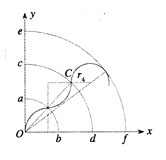
由几何关系知: ![]()
整理得: ![]()
则有: ![]()
为保证粒子不能从弧ef上射出磁场:
当III区域的磁场方向垂直坐标平面向里时,磁感应强度须满足![]()
当III区域的磁场方向垂直坐标平面向凶时,磁感应强度须满足![]()

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案