题目内容
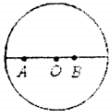湖面上一点O上下振动，振幅为0.2m，以O点为圆心形成的圆形水波，如图所示，A、B、O三点在一条直线上，OA间距离为4.0m，OB间距离为2.4m．某时刻O点处在波峰位置，观察发现2s后此波峰传到A点，此时O点正通过平衡位置向下运动，OA间还有一个波峰．将水波近似为简谐波．则此水波的传播速度=分析：由题意可知波传播的距离及所用时间，由波速公式可求得波的传播速度；由OA间对应的波长数可求得波长，由波长、频率及波速的关系可求得周期；
解答：解：波速v=
=
m/s=2m/s
由题意可知OA间相距
个波长，则对应
个周期；故由△t=
T可得：
周期T=1.6s；
则波长λ=vT=3.2m；
故答案为：2m/s，1.6s，3.2m
| △x |
| △t |
| 4 |
| 2 |
由题意可知OA间相距
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
周期T=1.6s；
则波长λ=vT=3.2m；
故答案为：2m/s，1.6s，3.2m
点评：本题要求学生能熟练掌握波的图象的性质，由波的图象可以判断各质点的振动方向、波长及振幅，然后才能由波长、频率及波速的关系求出要求的量．
练习册系列答案
相关题目
一兴趣小组的同学们观察到湖面上一点O上下振动，振幅为0.2m，以O点为圆心形成圆形水波，如图所示，A、B、O三点在一条直线上，OA间距离为4.0m，OB间距离为2.4m．某时刻O点处在波峰位置，观察发现2s后此波峰传到A点，此时O点正通过平衡位置向下运动，OA间还有一个波峰．将水波近似为简谐波．则以下说法正确的是（ ）
（2007?山东）物理--物理3-4
如图所示，湖面上一点O上下振动，振幅为0.2 m，以O点为圆心形成圆形水波， A、B、O三点在一条直线上，OA间距离为4.0 m，OB间距离为2.4 m。某时刻O点处在波峰位置，2s后此波峰传到A点，此时O点正通过平衡位置向下运动，OA间还有一个波峰。将水波近似为简谐波，则以下说法正确的是 （ ）