题目内容
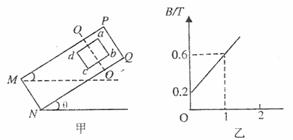
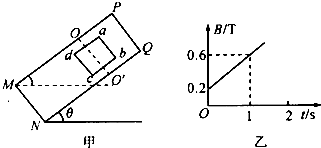
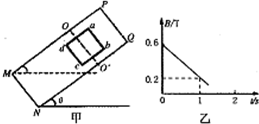
如图甲所示，PQNM是表面粗糙的绝缘斜面，abcd是质量m=0.5 kg、总电阻R=0.5 Ω、边长L=0.5 m的正方形金属线框，线框的匝数N=10。将线框放在斜面上，使斜面的倾角θ由0°开始缓慢增大，当θ增大到37°时，线框即将沿斜面下滑，假设最大静摩擦力与滑动摩擦力大小相等，现保持斜面的倾角θ=37°不变，在OO'NM的区域加上垂直斜面方向的匀强磁场，使线框的一半处于磁场中，磁场的磁感应强度B随时间t变化的图象如图乙所示。（g取10 m/s2，sin37°=0.6）
(1)试根据图乙写出B随时间t变化的函数关系式；
(2)请通过计算判断在t=0时刻线框是否会沿斜面运动？若不运动，请求出从t=0时刻开始经多长时间线框即将发生运动。
(1)试根据图乙写出B随时间t变化的函数关系式；
(2)请通过计算判断在t=0时刻线框是否会沿斜面运动？若不运动，请求出从t=0时刻开始经多长时间线框即将发生运动。
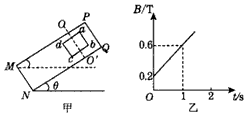
解：(1)由图乙所示图线可知：磁感应强度B随时间t均匀增大，所以B=B0+kt，其中B0=0.2 T，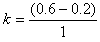
T/S= 0.4 T/s
所以B=0.2+0.4t (T)
(2)不加磁场时，由题意知，当θ=37°时，线框即将沿斜面下滑，此时斜面对线框的静摩擦力恰好达到最大值fmax，由平衡条件有
fmax=mgsinθ=0.6mg=3 N
加磁场后，由于压力不变，故fmax的大小不变，无论磁场方向垂直斜面向上还是向下，由楞次定理可知，当穿过线框的磁通量增大时，线框受到的安培力沿斜面向上，因此线框若是运动，则应沿斜面向上。即：满足F安≥mgsinθ+fmax=6 N
由法拉第电磁感应定律有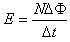
=
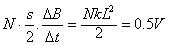
由闭合电路欧姆定律知，电流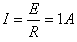
在t=0时刻cd边受到的安培力F0=NILB0=1 N
故F0＜mgsinθ+fmax，所以在t=0时刻，线框不会沿斜面下滑，也不会沿斜面上滑；当摩擦力方向沿斜面向下达到最大值时，线框即将沿斜面向上运动，此时线框受力如图所示，由平衡条件有
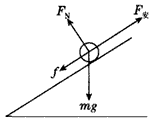
F安=NILB=mgsinθ+fmax=6N
得磁感应强度大小为B=1.2 T
由(1)知，B=0.2+0.4t (T)
则所经历时间为t=2.5 s
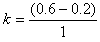T/S= 0.4 T/s所以B=0.2+0.4t (T)
(2)不加磁场时，由题意知，当θ=37°时，线框即将沿斜面下滑，此时斜面对线框的静摩擦力恰好达到最大值fmax，由平衡条件有
fmax=mgsinθ=0.6mg=3 N
加磁场后，由于压力不变，故fmax的大小不变，无论磁场方向垂直斜面向上还是向下，由楞次定理可知，当穿过线框的磁通量增大时，线框受到的安培力沿斜面向上，因此线框若是运动，则应沿斜面向上。即：满足F安≥mgsinθ+fmax=6 N
由法拉第电磁感应定律有
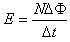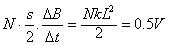
= 由闭合电路欧姆定律知，电流
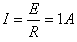
在t=0时刻cd边受到的安培力F0=NILB0=1 N
故F0＜mgsinθ+fmax，所以在t=0时刻，线框不会沿斜面下滑，也不会沿斜面上滑；当摩擦力方向沿斜面向下达到最大值时，线框即将沿斜面向上运动，此时线框受力如图所示，由平衡条件有
F安=NILB=mgsinθ+fmax=6N
得磁感应强度大小为B=1.2 T
由(1)知，B=0.2+0.4t (T)
则所经历时间为t=2.5 s
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图甲所示，PQNM是表面粗糙、倾角为θ=37°的绝缘斜面，abcd是质量m=0.5kg、总电阻R=0.5Ω、边长L=0.5m的正方形金属线框，线框的匝数N=5．将线框放在斜面上，不加磁场时两者之间的最大静摩擦力为3.7N．已知线框与斜面间的动摩擦因数μ=0.8．在OO′NM的长方形区域加上垂直斜面方向的匀强磁场，使线框面积的五分之二处于磁场中，磁场的磁感应强度B随时间t变化的图象如图乙所示（g取10m/s2，sin37°=0.6，cos37°=0.8）．
