题目内容
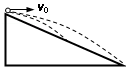
斜向上抛出一球,抛射角α=60°,当t=1秒时,球仍斜向上升,但方向已跟水平成β=45°角.(g取10 m/s2)
(1)球的初速度v0是多少?
(2)球将在什么时候达到最高点?
(1)球的初速度v0是多少?
(2)球将在什么时候达到最高点?
(1)10(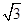 +1)m/s (2)
+1)m/s (2)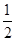 (3+
(3+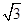 )s
)s
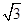 +1)m/s (2)
+1)m/s (2)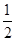 (3+
(3+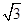 )s
)s(1)斜抛物体经t秒时在x、y方向的分速度vx=v0cos α,vy=v0sin α-gt.
当t=1秒时速度与水平方向夹角为β=45°,即
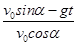 =tan45°,
=tan45°,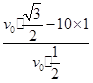 =1,
=1,
得v0=10(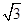 +1)m/s.
+1)m/s.
(2)设经过时间t到达最高点,
则vy=v0sin α-gt=0,
10(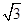 +1)×
+1)×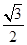 -10t=0,t=
-10t=0,t=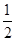 (3+
(3+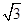 )s.
)s.
当t=1秒时速度与水平方向夹角为β=45°,即
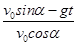 =tan45°,
=tan45°,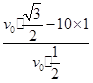 =1,
=1,得v0=10(
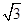 +1)m/s.
+1)m/s.(2)设经过时间t到达最高点,
则vy=v0sin α-gt=0,
10(
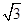 +1)×
+1)×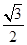 -10t=0,t=
-10t=0,t=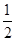 (3+
(3+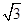 )s.
)s.
练习册系列答案
相关题目
以下有关运动的判断正确的是( )
| A.两个直线运动的合运动一定是直线运动 |
| B.做平抛运动的物体,任意相等时间内的速度变化相等 |
| C.只要物体做圆周运动,其加速度一定指向圆心 |
| D.匀速圆周运动的物体线速度保持不变 |