题目内容
（10分）如图19所示，在水平向左、电场强度为E的匀强电场中，竖直固定着一根足够长的粗糙绝缘杆，杆上套着一个质量为m、带有电荷量-q的小圆环，圆环与杆间的动摩擦因数为μ。
（1）由静止释放圆环，圆环沿杆下滑，求圆环下滑过程中受到的摩擦力f；
（2）若在匀强电场E的空间内再加上磁感应强度为B、方向垂直纸面向里的匀强磁场，圆环仍由静止开始沿杆下滑。求：
①圆环刚开始运动时加速度a0的大小；
②圆环下滑过程中的最大动能Ek。
【答案】
（1）
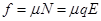（2）
【解析】
试题分析：（1）在水平方向圆环受到的弹力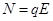
则摩擦力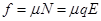
（3分）
（2）①圆环刚开始运动时不受洛伦兹力，因此，摩擦力大小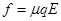
在竖直方向，由牛顿第二定律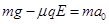 
（1分）
解得
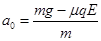（2分）
②当重力与滑动摩擦力平衡时，圆环速度最大，动能最大。
即
（1分）
最大速度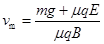
（2分）
最大动能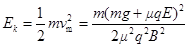
（1分）
考点：带电粒子在匀强电场中的运动
练习册系列答案
相关题目
（18分）如图18所示，上海磁悬浮列车专线西起上海地铁2号线的龙阳路站，东至上海浦东国际机场，专线全长29．863公里。由中德两国合作开发的世界第一条磁悬浮商运线。
（3）当金属框始终受到1N的阻力时，要使金属框维持最大速度，每秒钟需要消耗多少能量？这些能量是谁提供的？
，现用水平细绳将木块I固定在左边的墙上，传送带按图示方向匀速运动，则（ ）
如图19所示，在水平传送带上有三个质量分别为m、2m、3m的木块1、2、3，
中间分别用原长均为L、劲度系数均为k的相同轻弹簧连接起来，木块与传送带间的动摩擦因数为
，现用水平细绳将木块I固定在左边的墙上，传送带按图示方向匀速运动，则（ ）
| A．当三个木块达到平衡后，1、2两木块之间的距离是L+5mg/k |
| B．如果传送带的速率加倍同，1、2两木块之间的距离将加倍 |
| C．如果将细线剪断，那么木块2的瞬间加速度大小为0 |
| D．2、3间弹簧的弹性势能大于1、2间弹簧的弹性势能 |