题目内容
7.如图所示,间距为d的水平长直导轨MN、PQ与半径为r=1.0m的光滑圆轨道O1、O2平滑相接于P、M两点,在直导轨的N、Q间接阻值为R的电阻,宽度为L的abcd区域存在竖直导轨平面向下的匀强磁场(图中未画出),cd边界的左侧粗糙,右侧光滑,cd边界距PM的距离为S,一质量为m,电阻为R0的金属导体棒在外力F作用下以加速度a从静止开始匀加速运动到导轨P、M端时立即将外力F撤去.已知导体棒质量为m=1.0kg,导体棒与水平导轨的动摩擦因素μ=0.4,磁感应强度B=1.0T,电阻R=R0=2.0Ω(其余电阻不计),外力F与时间t的关系图象如图乙所示.(g取10m/s2)求:
(1)求导体棒在磁场区域运动的加速度a和长直导轨的间距d
(2)若金属棒不脱离圆轨道,试讨论S与导体棒上升的最大高度的关系.
分析 (1)由法拉第电磁感应定律、闭合电路欧姆定律、安培力公式F安=BId和牛顿第二定律得到F与t的关系式,结合图象的信息求解.
(2)若金属棒不脱离圆轨道,有两种情况:一、导体棒刚好到达圆轨道与圆心等高点位置;二、导体棒能到达圆轨道的最高点.根据临界条件和动能定理结合解答.
解答 解:(1)导体棒做匀加速直线运动,且切割磁感线,由法拉第电磁感应定律得感应电动势为:
E=Bdv…①
由闭合电路欧姆定律得通过导体棒的感应电流为:$I=\frac{E}{{R+{R_0}}}$…②
导体棒穿过磁场过程中受到的安培力为:F安=BId…③
由牛顿第二定律得:F-F安=ma…④
由 ①②③④式联立解得:$F=ma+\frac{{{B^2}{d^2}a}}{{R+{R_0}}}t$…⑤
代入数据得:$F=a+\frac{{a{d^2}}}{4}t$…⑥
由图乙可知,a=2m/s2;$\frac{a{d}^{2}}{4}$=2…⑧
解得:d=2m…⑨
(2)设导体棒刚离开磁场区域时的速度为v0,由匀变速运动规律得:v0=at=4m/s…⑩
导体棒离开磁场后做匀加速直线运动,到达P、M端点时设速度为为v1,由动能定理得:
$(F-μmg)S=\frac{1}{2}m{v_1}^2-\frac{1}{2}m{v_0}^2$…(11)
解得:${v_1}=2\sqrt{S+4}$…(12)
讨论一:若导体棒刚好到达圆轨道与圆心等高点位置,则须满足:$\frac{1}{2}m{v_1}^2≤mgr$…(13)
解得:S≤1.0m
设导体棒上升的最大高度为h,由动能定理得:$mgh=\frac{1}{2}m{v_1}^2$…(14),
解得:h=0.8+0.2S…(15)
讨论二:若导体棒能到达圆轨道的最高点,则须满足 $mg≥\frac{{m{v_2}^2}}{r}$…(16)
由动能定理得:$mg2r≤\frac{1}{2}m{v_1}^2-\frac{1}{2}m{v_2}^2$…(17),
解得:S≥8.5m…(18)
则导体棒上升的最大高度为:h=2r=2.0m…(19).
答:(1)导体棒在磁场区域运动的加速度a是2m/s2;长直导轨的间距d是2m.
(2)若金属棒不脱离圆轨道,S与导体棒上升的最大高度的关系为:若导体棒刚好到达圆轨道与圆心等高点位置时,h=0.8+0.2S;若导体棒能到达圆轨道的最高点时导体棒上升的最大高度为 h=2r=2.0m.
点评 本题是电磁感应与力学的综合,关键要正确分析导体棒可能的运动情形,抓住圆周运动的条件,由力学规律和电磁感应规律结合解答.


| A. | 沿y轴方向做匀速运动 | B. | 沿x轴方向做匀速运动 | ||
| C. | 沿y轴方向做匀加速运动 | D. | 沿x轴方向做匀加速运动 |
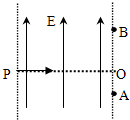 如图所示,不计重力的两个质量相同的带电粒子,以相同的速度从P点水平射入一个有边界、方向竖直向上的匀强电场中,分别从A点和B点离开电场,且AO<BO,下列判断正确的是( )
如图所示,不计重力的两个质量相同的带电粒子,以相同的速度从P点水平射入一个有边界、方向竖直向上的匀强电场中,分别从A点和B点离开电场,且AO<BO,下列判断正确的是( )| A. | 两个粒子电性相反 | |
| B. | 两个粒子在电场中运动的时间不一样 | |
| C. | 两个粒子做匀速圆周运动 | |
| D. | 两个粒子的电势能均减小 |
 研究自由落体运动时,起始点O到D的时间为t,计数点A、B、C、D各点相邻时间间隔为T,为了计算纸带上C点时的重物的速度大小,其中正确的是( )
研究自由落体运动时,起始点O到D的时间为t,计数点A、B、C、D各点相邻时间间隔为T,为了计算纸带上C点时的重物的速度大小,其中正确的是( )| A. | υC=$\sqrt{2g{h}_{3}}$ | B. | υC=gt | C. | υC=$\frac{{h}_{4}-{h}_{2}}{2T}$ | D. | υC=$\frac{{h}_{4}-{h}_{3}}{T}$ |
 一质量为2kg的物体,在水平恒定拉力的作用下以一定的初速度在粗糙的水平面上做匀速运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图中给出了拉力随位移变化的关系图象.已知重力加速度
一质量为2kg的物体,在水平恒定拉力的作用下以一定的初速度在粗糙的水平面上做匀速运动,当运动一段时间后,拉力逐渐减小,且当拉力减小到零时,物体刚好停止运动,图中给出了拉力随位移变化的关系图象.已知重力加速度g=10m/s2,由此可知( )
| A. | 物体与水平面间的动摩擦因数约为0.5 | |
| B. | 减速过程中拉力对物体所做的功约为10J | |
| C. | 匀速运动时的速度约为6m/s | |
| D. | 减速运动的时间约为1.7s |
| A. | 黑体辐射的强度与频率的关系是:随着温度的升高,各种频率的辐射都增加,辐射强度极大值的光向频率较低的方向移动 | |
| B. | α粒子散射实验中少数α粒子发生了较大偏转是卢瑟福猜想原子核式结构模型的主要依据 | |
| C. | 天然放射现象的发现说明了原子有复杂的结构 | |
| D. | 利用α射线可发现金属制品中的裂纹 |
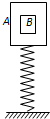 如图所示,一轻弹簧直立地面上,其劲度系数为400N/m,弹簧上端与盒子A连接在一起,盒子内装物体B,B的上下表面恰与盒子接触,A和B的质量mA=mB=1.0kg,g=10m/s2,不计空气阻力.先将A向上抬高使弹簧伸长5.0cm后,从静止释放,释放后A和B一起做简谐运动.试求:
如图所示,一轻弹簧直立地面上,其劲度系数为400N/m,弹簧上端与盒子A连接在一起,盒子内装物体B,B的上下表面恰与盒子接触,A和B的质量mA=mB=1.0kg,g=10m/s2,不计空气阻力.先将A向上抬高使弹簧伸长5.0cm后,从静止释放,释放后A和B一起做简谐运动.试求:
 如图所示是利用光电门探究“滑块加速度与外力关系”的实验装置.实验中,将力传感器固定在滑块上,然后把绳的一端固定在传感器的挂钩上,用来测量绳对滑块的拉力,探究在滑块及传感器总质量不变时加速度跟它们所受拉力的关系.本实验,若平衡摩擦力后还需要直接测量的物理量有:滑块上的挡光板的宽度为d,滑块出发点到光电门位置距离为l,使滑块从起点由静止开始运动,光电计时器记录下滑块上挡光板通过光电门的时间为△t.
如图所示是利用光电门探究“滑块加速度与外力关系”的实验装置.实验中,将力传感器固定在滑块上,然后把绳的一端固定在传感器的挂钩上,用来测量绳对滑块的拉力,探究在滑块及传感器总质量不变时加速度跟它们所受拉力的关系.本实验,若平衡摩擦力后还需要直接测量的物理量有:滑块上的挡光板的宽度为d,滑块出发点到光电门位置距离为l,使滑块从起点由静止开始运动,光电计时器记录下滑块上挡光板通过光电门的时间为△t.