题目内容
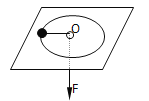
【题目】如图所示，在水平放置的光滑板中心开一光滑小孔O，从小孔中穿过一细绳，绳的一端系一个小球，另一端用力F拉着使球在平板上做半径为r=40cm角速度ω=2.5rad/s的匀速圆周运动，在运动过程中若迅速松开绳子至小球与O点的距离R=50cm时又迅速拉紧绳子，小球就能在以半径为R的圆周上做匀速圆周运动.则（ ）
A. 小球由半径r变化到R所需的时间为0.15s
B. 小球由半径r变化到R所需的时间为0.30s
C. 小球在半径为R的圆周上运动的角速度为1.6rad/s
D. 小球在半径为R的圆周上运动的角速度为2.0rad/s
【答案】BC
【解析】试题分析：绳子放开后，质点沿切线方向飞出，做匀速直线运动，结合几何关系，可求运动时间；绳子放开后，质点沿切线方向飞出，做匀速直线运动，到绳子突然张紧时，将速度沿切线方向和半径方向正交分解，沿半径方向的分速度突然减为零，以切线方向的分速度绕R轨道匀速圆周运动，由牛顿第二定律和线速度与角速度的关系公式可求出角速度的大小．
小球以半径r运动时的线速度为
，松开后，小球以速度
沿半径r的切线向外运动，运动位移为
，所以小球由半径r变化到R所需的时间为
，A错误B正确；小球沿圆弧切线方向飞出后，到达R轨道时，绳子突然张紧，将速度沿切线方向和半径方向正交分解，沿半径方向的分速度突然减为零，以切线方向的分速度绕R轨道匀速圆周运动，由几何关系得到，由
，则角速度
，故C正确D错误．
练习册系列答案
名校课堂系列答案
相关题目
