��Ŀ����
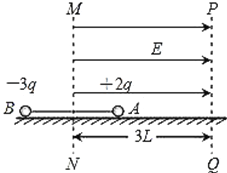
����Ŀ����ͼ��ʾ���ڹ⻬��Ե��ˮƽ���ϣ��ó�Ϊ2L�ľ�Ե�����������������Ϊm�Ĵ���С��A��B��A��Ĵ�����Ϊ+2q��B��Ĵ�����Ϊ��3q���������һ����ϵͳ������MN��PQƽ�������3L����ʼʱA��B�ֱ�ֹ������MN�����࣬����MNǡΪAB�������ߵĴ�ֱƽ���ߣ�����С��Ϊ�ʵ㣬������˵�������������MN��PQ�����ˮƽ���ҵĵ糡ǿ��ΪE����ǿ�糡������
(1)B��ս���糡ʱ������ϵͳ���ٶȴ�С��
(2)����ϵͳ�����˶���������ʹ˹�����B������ܵı仯����
(3)����ϵͳ�˶������ڣ�
���𰸡�(1) ![]() (2)
(2) ![]() ,
, ![]() (3)
(3) ![]()
����������1����B��ս���糡ʱ����ϵͳ�ٶ�Ϊv1���ɶ��ܶ�����2qEL��![]() 2mv12
2mv12
���![]()
��2������ϵͳ�����˶������Σ�B�����糡ǰ������ϵͳ�ڵ糡�С�A����糡��
��A����糡�����λ��Ϊx���ɶ��ܶ�����2qEL-qEL-3qEx=0
���x��![]()
��s��=![]()
B��Ӹս���糡������ϵͳ�ӿ�ʼ�˶����ٶȵ�һ��Ϊ��ʱλ��Ϊ![]() L
L
������ܵı仯��Ϊ��Ep��W��3qE![]() L��4qEL
L��4qEL
��3��ȡ����Ϊ������
��һ�μ���![]() ��
��![]()
�ڶ��μ���a2��![]()
��A��ճ��糡�ٶ�Ϊv2���ɶ��ܶ�����![]()
���v2��![]()
![]()
�������ټ���������ٶ�a3��ʱ��t3Ϊ�� ![]() ��
�� ![]()
���Դ���ϵͳ�˶�������Ϊ�� ![]() ��
��

 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д�