题目内容
 如图,在竖直平面内,光滑的圆弧轨道EA和BC与粗糙的水平轨道AB相切于A点和B点,相切处平滑.B是BC圆弧最低点,C与圆心O等高,BC圆弧半径R=1m.EA圆弧的半径r>2m,E是圆弧EA最高点,h=2m.现有一个质量为m=0.1kg的小物块(可视为质点),从C点的正上方D点处自由下落,DC距离H=4m,物块与水平面AB之间的动摩擦因数μ=0.5.取g=10m/s2.求:
如图,在竖直平面内,光滑的圆弧轨道EA和BC与粗糙的水平轨道AB相切于A点和B点,相切处平滑.B是BC圆弧最低点,C与圆心O等高,BC圆弧半径R=1m.EA圆弧的半径r>2m,E是圆弧EA最高点,h=2m.现有一个质量为m=0.1kg的小物块(可视为质点),从C点的正上方D点处自由下落,DC距离H=4m,物块与水平面AB之间的动摩擦因数μ=0.5.取g=10m/s2.求:(1)物块到达B点时轨道对物块的支持力FN的大小.
(2)要使物块不从E点飞出,AB的长度LAB至少要多长.
分析:(1)对D到B段运用动能定理,求出到达B点的速度,根据牛顿第二定律求出支持力的大小.
(2)对D→C→B→A→E全过程运用动能定理,抓住E点临界速度为零,求出AB的至少长度.
(2)对D→C→B→A→E全过程运用动能定理,抓住E点临界速度为零,求出AB的至少长度.
解答:解:(1)小球从D到B,由机械能守恒得:mg(H+R)=
mvB2①
在B点,由牛顿第二定律得:FN-mg=m
②
联立①、②解得 FN=11 N ③
(2)要使小球不从E点飞出的临界条件是小球到达E点速度必须为零
从D→C→B→A→E全过程,由动能定理得
mg (H+R-h)-mg μLAB=0④
解得LAB=6m
所以,AB的长度LAB至少6m
答:(1)物块到达B点时轨道对物块的支持力FN的大小为11N.
(2)要使物块不从E点飞出,AB的长度LAB至少要6m.
| 1 |
| 2 |
在B点,由牛顿第二定律得:FN-mg=m
| vB2 |
| R |
联立①、②解得 FN=11 N ③
(2)要使小球不从E点飞出的临界条件是小球到达E点速度必须为零
从D→C→B→A→E全过程,由动能定理得
mg (H+R-h)-mg μLAB=0④
解得LAB=6m
所以,AB的长度LAB至少6m
答:(1)物块到达B点时轨道对物块的支持力FN的大小为11N.
(2)要使物块不从E点飞出,AB的长度LAB至少要6m.
点评:本题综合考查了动能定理和牛顿第二定律,运用动能定理解题注意选择合适的研究过程,列式进行求解.

练习册系列答案
相关题目
 如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的3/4圆弧轨道,两轨道相切与B点.在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g.求:
如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的3/4圆弧轨道,两轨道相切与B点.在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力.已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g.求: 如图,在竖直平面内有一固定光滑轨道,其中AB部分是倾角为37°的直轨道,BCD部分是以O为圆心、半径为R的圆弧轨道,两轨道相切于B点,D点与O点等高,A点在D点的正下方.质量为m的小球在沿斜面向上的拉力F作用下,从A点由静止开始做变加速直线运动,到达B点时撤去外力.已知小球刚好能沿圆轨道经过最高点C,然后经过D点落回到A点.已知sin37°=0.6,cos37°=0.8,重力加速度大小为g.求
如图,在竖直平面内有一固定光滑轨道,其中AB部分是倾角为37°的直轨道,BCD部分是以O为圆心、半径为R的圆弧轨道,两轨道相切于B点,D点与O点等高,A点在D点的正下方.质量为m的小球在沿斜面向上的拉力F作用下,从A点由静止开始做变加速直线运动,到达B点时撤去外力.已知小球刚好能沿圆轨道经过最高点C,然后经过D点落回到A点.已知sin37°=0.6,cos37°=0.8,重力加速度大小为g.求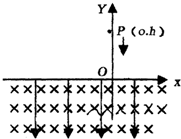 如图,在竖直平面内x轴下方有磁感强度为B,方向垂直纸面向里的匀强磁场和竖直向下的匀强电场,电场强度为E,一个带电小球从y轴上P(o.h)点以初速V0竖直向下抛出,小球穿过x轴后恰好作匀速圆周运动,重力加速度为g.求:(不知小球质量和电量)
如图,在竖直平面内x轴下方有磁感强度为B,方向垂直纸面向里的匀强磁场和竖直向下的匀强电场,电场强度为E,一个带电小球从y轴上P(o.h)点以初速V0竖直向下抛出,小球穿过x轴后恰好作匀速圆周运动,重力加速度为g.求:(不知小球质量和电量)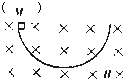 如图,在竖直平面内放一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道E在的平面垂直.一个带负电荷的小滑块由静止开始从半圆轨道的最高点M滑下,则下列说法中正确的是( )
如图,在竖直平面内放一个光滑绝缘的半圆形轨道,水平方向的匀强磁场与半圆形轨道E在的平面垂直.一个带负电荷的小滑块由静止开始从半圆轨道的最高点M滑下,则下列说法中正确的是( )