题目内容
3.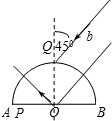 半径为R的半圆柱形介质截面如图所示,O为圆心,AB为直径,Q是半圆O上的一点,QO垂直于AB.相互平行的同种单色光a和b,从不同位置进入介质,光线a沿直线射向O点,在O点恰好发生全反射,光线b从Q点射入介质,入射角为45°.b光经介质折射后交于直径AB上的P点,则P点距O点的距离为( )
半径为R的半圆柱形介质截面如图所示,O为圆心,AB为直径,Q是半圆O上的一点,QO垂直于AB.相互平行的同种单色光a和b,从不同位置进入介质,光线a沿直线射向O点,在O点恰好发生全反射,光线b从Q点射入介质,入射角为45°.b光经介质折射后交于直径AB上的P点,则P点距O点的距离为( )| A. | $\frac{\sqrt{3}}{3}$R | B. | $\frac{\sqrt{2}}{2}$R | C. | $\frac{\sqrt{3}}{2}$R | D. | $\frac{1}{2}$R |
分析 根据光线a在AB面上发生全反射,结合sinC=$\frac{1}{n}$求出折射率,从而通过折射定律求出b光线在半圆柱面上的折射角,根据几何关系求出P点距O点的距离.
解答 解:光线a在AB面上发生全反射,根据sinC=$\frac{1}{n}$得,C=45°,解得折射率n=$\sqrt{2}$.
根据折射定律知,$\frac{sin45°}{sinθ}=\sqrt{2}$,解得b光在半圆柱面上的折射角θ=30°,
设P点距O为x,根据几何关系知,$tan30°=\frac{x}{R}$,解得x=$\frac{\sqrt{3}}{3}R$.故A正确,B、C、D错误.
故选:A.
点评 本题是简单的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,根据折射定律求解.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
14. 如图所示,两端开口的U形管,右侧直管中有一部分空气被一 段水银柱与外界隔开,若在左管中再注入一些水银,平衡后则( )
如图所示,两端开口的U形管,右侧直管中有一部分空气被一 段水银柱与外界隔开,若在左管中再注入一些水银,平衡后则( )
 如图所示,两端开口的U形管,右侧直管中有一部分空气被一 段水银柱与外界隔开,若在左管中再注入一些水银,平衡后则( )
如图所示,两端开口的U形管,右侧直管中有一部分空气被一 段水银柱与外界隔开,若在左管中再注入一些水银,平衡后则( )| A. | 下部两侧水银面A、B高度差h减小 | B. | h增大 | ||
| C. | 右侧封闭气柱体积变小 | D. | 水银面A、B高度差h不变 |
11.下列说法正确的是( )
| A. | 曲线运动一定是变速运动 | |
| B. | 曲线运动一定是非匀变速运动 | |
| C. | 匀速圆周运动是速度不变的运动 | |
| D. | 分运动是直线运动,合运动一定是直线运动 |
18. 宋代诗人陈与义乘着小船在风和日丽的春日出游时曾写下了一首诗,在这首诗中,诗人艺术性地描述了他对运动的相对性的理解.下列说法正确的是( )
宋代诗人陈与义乘着小船在风和日丽的春日出游时曾写下了一首诗,在这首诗中,诗人艺术性地描述了他对运动的相对性的理解.下列说法正确的是( )
 宋代诗人陈与义乘着小船在风和日丽的春日出游时曾写下了一首诗,在这首诗中,诗人艺术性地描述了他对运动的相对性的理解.下列说法正确的是( )
宋代诗人陈与义乘着小船在风和日丽的春日出游时曾写下了一首诗,在这首诗中,诗人艺术性地描述了他对运动的相对性的理解.下列说法正确的是( )| A. | 第三句选择的参考系为大地 | B. | 第四句选择的参考系为云 | ||
| C. | 第四句选择的参考系为“我” | D. | 第三句选择的参考系为“我” |
8.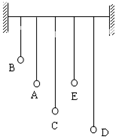 如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则( )
如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则( )
 如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则( )
如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则( )| A. | 其它各摆摆动周期跟A摆相同 | B. | 其它各摆振动振幅大小相同 | ||
| C. | 其它各摆振动振幅大小不相同 | D. | D摆振幅最大 |
12.平行板电容器充电后,与电池两极断开连接,当两极板间的距离减小时( )
| A. | 电容器两极板间的电场强度变大 | B. | 电容器极板的带电量变大 | ||
| C. | 电容器两极板间的电势差变大 | D. | 电容器的电容变大 |
13.下列说法中不正确的是( )
| A. | 只有平面波的波面才与波线垂直 | B. | 任何波的波线与波面都相互垂直 | ||
| C. | 任何波的波线表示波的传播方向 | D. | 有些波的波面表示波的传播方向 |

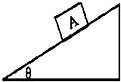 如图,倾角θ=30°的斜面固定在水平地面上,物块A重力G=20N,物块与斜面间的动摩擦因数μ=0.8,物块放在斜面上.试求:
如图,倾角θ=30°的斜面固定在水平地面上,物块A重力G=20N,物块与斜面间的动摩擦因数μ=0.8,物块放在斜面上.试求: