Question

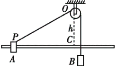
【题目】如图所示，航天飞机在完成对哈勃空间望远镜的维修任务后，在A点从圆形轨道Ⅰ进入椭圆轨道Ⅱ，B为轨道Ⅱ上的一点，关于航天飞机的运动，下列说法中正确的是

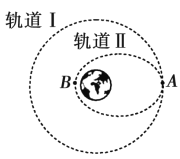
A. 在轨道Ⅱ上经过A的速度大于经过B的速度

B. 在轨道Ⅱ上经过A的动能大于在轨道I上经过A的动能

C. 在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期

D. 在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度

Answer 1

【答案】C

【解析】

A.轨道Ⅱ上由A点运动到B点，引力做正功，动能增加，所以经过A的速度小于经过B的速度。故A错误。

B.从轨道Ⅰ的A点进入轨道Ⅱ需减速，使万有引力大于所需要的向心力，做近心运动。所以轨道Ⅱ上经过A的速度小于在轨道Ⅰ上经过A的速度，则在轨道Ⅱ上经过A的动能小于在轨道Ⅰ上经过A的动。故B错误。

C.根据开普勒第三定律＝C，椭圆轨道的半长轴小于圆轨道的半径，所以在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期。故C正确。

D.由可得在轨道Ⅱ上和在轨道Ⅰ通过A点距离地心的距离r相等，因此所受的万有引力相等，根据牛顿第二定律，加速度相等。故D错误。