题目内容
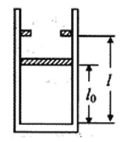
【题目】如图所示,水平轨道![]() 的左端与固定的光滑竖直
的左端与固定的光滑竖直![]() 圆轨道相切于
圆轨道相切于![]() 点,右端与一倾角为
点,右端与一倾角为![]() 的光滑斜面轨道在
的光滑斜面轨道在![]() 点平滑连接(即物体经过
点平滑连接(即物体经过![]() 点时速度的大小不变),斜面顶端固定一轻质弹簧,一质量为
点时速度的大小不变),斜面顶端固定一轻质弹簧,一质量为![]() 的滑块从圆弧轨道的顶端
的滑块从圆弧轨道的顶端![]() 点由静止释放,经水平轨道后滑上斜面并压缩弹簧,第一次可将弹簧压缩至
点由静止释放,经水平轨道后滑上斜面并压缩弹簧,第一次可将弹簧压缩至![]() 点,已知光滑圆轨道的半径
点,已知光滑圆轨道的半径![]() ,水平轨道
,水平轨道![]() 长为
长为![]() ,其动摩擦因数
,其动摩擦因数![]() ,光滑斜面轨道上
,光滑斜面轨道上![]() 长为
长为![]() ,
,![]() 取
取![]() ,求
,求

(1)滑块第一次经过圆轨道上![]() 点时对轨道的压力大小;
点时对轨道的压力大小;
(2)整个过程中弹簧具有最大的弹性势能;
(3)滑块在水平轨道![]() 上运动的总时间及滑块几次经过
上运动的总时间及滑块几次经过![]() 点.
点.
【答案】(1)![]() (2)
(2)![]() (3) 3次
(3) 3次
【解析】本题考查机械能与曲线运动相结合的问题,需运用动能定理、牛顿运动定律、运动学公式、功能关系等知识。
(1)滑块从![]() 点到
点到![]() 点,由动能定理可得:
点,由动能定理可得:![]()
解得: ![]()
滑块在![]() 点:
点: ![]()
解得: ![]()
由牛顿第三定律可得:物块经![]() 点时对轨道的压力
点时对轨道的压力![]()
(2)滑块第一次到达![]() 点时,弹簧具有最大的弹性势能
点时,弹簧具有最大的弹性势能![]() .滑块从
.滑块从![]() 点到
点到![]() 点,由动能定理可得:
点,由动能定理可得: ![]()
![]()
解得: ![]()
(3)将滑块在![]() 段的运动全程看作匀减速直线运动
段的运动全程看作匀减速直线运动
加速度![]()
则滑块在水平轨道![]() 上运动的总时间
上运动的总时间![]()
滑块最终停止上在水平轨道![]() 间,设滑块在
间,设滑块在![]() 段运动的总路程为
段运动的总路程为![]() ,从滑块第一次经过
,从滑块第一次经过![]() 点到最终停下来的全过程,
点到最终停下来的全过程,
由动能定理可得: ![]()
解得: ![]()
结合![]() 段的长度可知,滑块经过
段的长度可知,滑块经过![]() 点3次。
点3次。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目