题目内容
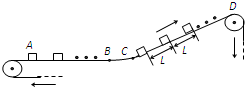
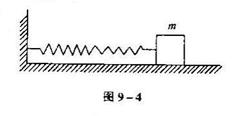
如图9-4所示,弹簧的一端固定在墙上。另一端连结一质量为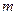 的木块,今将木块向右拉开一位移L后释放,木块在有摩擦的水平地面上减幅振动。弹簧第一次恢复原长时,木块速度为
的木块,今将木块向右拉开一位移L后释放,木块在有摩擦的水平地面上减幅振动。弹簧第一次恢复原长时,木块速度为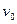 ,试讨论:木块在整个振动过程中出现速度为
,试讨论:木块在整个振动过程中出现速度为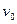 的位置有几个。
的位置有几个。
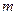 的木块,今将木块向右拉开一位移L后释放,木块在有摩擦的水平地面上减幅振动。弹簧第一次恢复原长时,木块速度为
的木块,今将木块向右拉开一位移L后释放,木块在有摩擦的水平地面上减幅振动。弹簧第一次恢复原长时,木块速度为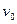 ,试讨论:木块在整个振动过程中出现速度为
,试讨论:木块在整个振动过程中出现速度为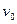 的位置有几个。
的位置有几个。
在整个振动过程中出现速度为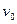 的位置有,且只有2个。
的位置有,且只有2个。
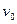 的位置有,且只有2个。
的位置有,且只有2个。放手后,木块在水平方向上的弹力和摩擦力同时作用下,先向左作加速度变小的加速运动。后向左作加速度变大的减速运动。在原平衡位置右侧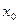 处(
处(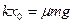 ),一定存在一加速度为零的位置,此位置向左的速度最大。根据速度变化必须是连续的原理可知,既然左侧有一
),一定存在一加速度为零的位置,此位置向左的速度最大。根据速度变化必须是连续的原理可知,既然左侧有一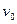 ,其右侧也一定存在一
,其右侧也一定存在一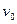 的位置。
的位置。
此后的运动,可从能量角度分析不会再有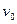 的位置出现。
的位置出现。
因为在弹簧第一次恢复原长,木块速度为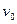 时,系统振动的能量
时,系统振动的能量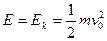 ,此后的运动仍属阻尼振动,由于摩擦的作用振动能量不断减小,
,此后的运动仍属阻尼振动,由于摩擦的作用振动能量不断减小,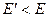 ,设此后振动中任一时刻的速率为
,设此后振动中任一时刻的速率为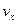 ,
,
即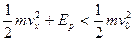
所以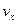 必小于
必小于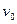 ,且不断变小,直至停止振动为止。
,且不断变小,直至停止振动为止。
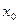 处(
处(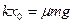 ),一定存在一加速度为零的位置,此位置向左的速度最大。根据速度变化必须是连续的原理可知,既然左侧有一
),一定存在一加速度为零的位置,此位置向左的速度最大。根据速度变化必须是连续的原理可知,既然左侧有一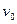 ,其右侧也一定存在一
,其右侧也一定存在一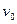 的位置。
的位置。此后的运动,可从能量角度分析不会再有
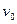 的位置出现。
的位置出现。因为在弹簧第一次恢复原长,木块速度为
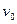 时,系统振动的能量
时,系统振动的能量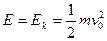 ,此后的运动仍属阻尼振动,由于摩擦的作用振动能量不断减小,
,此后的运动仍属阻尼振动,由于摩擦的作用振动能量不断减小,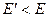 ,设此后振动中任一时刻的速率为
,设此后振动中任一时刻的速率为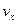 ,
,即
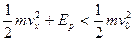
所以
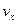 必小于
必小于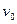 ,且不断变小,直至停止振动为止。
,且不断变小,直至停止振动为止。 
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
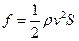 ,式中
,式中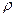 空气密度,S为等效受阻面积.求返回舱的质量是多大?
空气密度,S为等效受阻面积.求返回舱的质量是多大?