题目内容
 (2010?山东)渔船常利用超声波来探测远处鱼群的方位.已知某超声波频率为1.0×105Hz,某时刻该超声波在水中传播的波动图象如图所示.
(2010?山东)渔船常利用超声波来探测远处鱼群的方位.已知某超声波频率为1.0×105Hz,某时刻该超声波在水中传播的波动图象如图所示.①从该时刻开始计时,划出x=7.5×10-3m处质点做简谐运动的振动图象(至少一个周期).
②现测得超声波信号从渔船到鱼群往返一次所用时间为4s,求鱼群与渔船间的距离(忽略船和鱼群的运动).
分析:(1)由图读出振幅为A,波长为1.5×10-2 m,由频率求出周期T,此时x=7.5×10-3 m处的质点位于负的最大位移处,画出振动图象.
(2)由频率和波长求出波速v,根据信号从渔船到鱼群往返一次所用时间为4s,求出鱼群与渔船间的距离x=
vt.
(2)由频率和波长求出波速v,根据信号从渔船到鱼群往返一次所用时间为4s,求出鱼群与渔船间的距离x=
| 1 |
| 2 |
解答: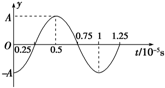 解:(1)该波的周期为T=
解:(1)该波的周期为T=
=1×10-5 s,
由波动图象知,此时x=7.5×10-3 m处的质点位于负的最大位移处,所以,从该时刻开始计时,该质点的振动图象,如图所示.
(2)由波形图读出波长λ=15×10-3 m
由波速公式得v=λf ①
鱼群与渔船的距离为x=
vt ②
联立①②式,代入数据得x=3000m.
答:(1)振动图象如图所示.
(2)鱼群与渔船的距离为3000m.
 解:(1)该波的周期为T=
解:(1)该波的周期为T=| 1 |
| f |
由波动图象知,此时x=7.5×10-3 m处的质点位于负的最大位移处,所以,从该时刻开始计时,该质点的振动图象,如图所示.
(2)由波形图读出波长λ=15×10-3 m
由波速公式得v=λf ①
鱼群与渔船的距离为x=
| 1 |
| 2 |
联立①②式,代入数据得x=3000m.
答:(1)振动图象如图所示.
(2)鱼群与渔船的距离为3000m.
点评:本题考查理解振动图象和波动图象联系的能力和作图能力.波在同一介质中认为是匀速传播的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?山东)如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出.
(2010?山东)如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出. (2010?山东)一太阳能空气集热器,底面及侧面为隔热材料,顶面为透明玻璃板,集热器容积为v0,开始时内部封闭气体的压强为po.经过太阳曝晒,气体温度由T0=300k升至T1=350K.
(2010?山东)一太阳能空气集热器,底面及侧面为隔热材料,顶面为透明玻璃板,集热器容积为v0,开始时内部封闭气体的压强为po.经过太阳曝晒,气体温度由T0=300k升至T1=350K. (2011?山东模拟)(1)渔船常利用超声波来探测远外鱼群的方位.已知某超声波频率为1.0×105Hz,某时刻该超声波在水中传播的波动图象如图所示.
(2011?山东模拟)(1)渔船常利用超声波来探测远外鱼群的方位.已知某超声波频率为1.0×105Hz,某时刻该超声波在水中传播的波动图象如图所示.