题目内容
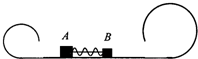如图所示，水平面上的A，B两物体中间有一被细线拉着的被压缩了的轻弹簧，两边是两个在竖直平面内的半径分别为R和2R圆弧形轨道．当细线突然断开后，两物体分别运动到轨道最高点时，对轨道的压力都为0．不计任何摩擦，求：A、B两物体的质量mA和mB之比．分析：能到达半圆形轨道最高点的临界条件是v≥
，恰好能通过最高点说明在最高点重力完全提供向心力，系统满足动量守恒，据此求解即可．
| gr |
解答：解：系统满足动量守恒得
mAvA=mBvB
最高点：对轨道的压力为0，所以根据牛顿第二定律：
A：mAg=
B：mBg=
根据动能定理有：
-
=2mAgR
-
=4mBgR
联立解得mA：mB=
：1
答：A、B两物体的质量mA和mB之比是
：1
mAvA=mBvB
最高点：对轨道的压力为0，所以根据牛顿第二定律：
A：mAg=
| ||
| R |
B：mBg=
| ||
| 2R |
根据动能定理有：
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
联立解得mA：mB=
| 2 |
答：A、B两物体的质量mA和mB之比是
| 2 |
点评：小球刚好到达圆管形轨道最高点的条件是：到达最高点时速度为零；应用牛顿第二定律、动量守恒定律即可正确解题．
练习册系列答案
初中暑期衔接系列答案
相关题目
如图所示，水平面上的O点处并放着AB两个物体，在A的左侧距A距离为x0处有一竖直挡板，AB之间有少量的炸药，爆炸后B以v2=2m/s的速度向右做匀减速运动，直到静止． A以v1=4m/s的速率向左运动，运动到挡板后与挡板发生时间极短的碰撞，碰撞后以碰撞前的速率返回，已知AB在运动过程中加速度大小均为a=1m/s2，方向与物体的运动方向始终相反，AB两物体均视为质点．计算：
如图所示为水平面上的物体在水平拉力F作用下的v-t 图线和拉力F的功率-时间图线，则物体跟水平面间的动摩擦因数为（g=10m/s2）（ ）
如图所示，水平面上的轻弹簧一端与物体相连，另一端固定在墙上的P点，已知物体的质量为m，物体与水平面间的动摩擦因数μ，弹簧的劲度系数k．现用力拉物体，使弹簧从处于自然状态的O点由静止开始缓慢向左移动一段距离，这时弹簧具有弹性势能Ep．撤去外力后，物体在O点两侧往复运动的过程中（ ）
如图所示，水平面上的轻弹簧一端与物体相连，另一端固定在墙上的P点，已知物体的质量为m=2.0kg，物体与水平面间的动摩擦因数μ=0.4，弹簧的劲度系数k=200N/m．现用力F拉物体，使弹簧从处于自然状态的O点由静止开始向左移动10cm，这时弹簧具有弹性势能Ep=1.0J，物体处于静止状态．若取g=10m/s2，则撤去外力F后（ ）