题目内容
如图所示,质量为M玻璃管中盛有少量乙醚液体,用质量为m的软木塞将管口封住,且M=3m,加热玻璃管使软木塞在乙醚蒸气的压力下水平飞出。玻璃管悬于长为L的轻杆上,轻杆可绕O端无摩擦转动(玻璃管本身几何大小忽略不计)。若在一次实验中,当软木塞水平飞出后玻璃管恰好能在竖直面内作圆周运动,在忽略热量损失和空气阻力的情况下,求:
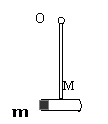
(1)乙醚要消耗多少内能;
(2)软木塞水平飞出瞬间杆对玻璃管拉力的大小。
(3)玻璃管通过最高点时杆对玻璃管力的大小和方向。
解:
(1)设软木塞水平飞出时,M和m的速率分别为V和v,对软木塞和玻璃管组成的系统在木塞飞出前后过程,由动量守恒定律得
MV-mv=0 ①
玻璃管恰能越过最高点做圆周运动的临界条件是在最高点的速度为零,由机械能守恒定律有 ![]() =Mg2L ②
=Mg2L ②
由能量转化和守恒定律可知,管塞分离时二者的动能之和都是由乙醚消耗其内能得来的,所以 E内=![]() +
+![]() =24mgL
=24mgL
(2)由②得M的速度V=![]() ,在最低点应用向心力公式得
,在最低点应用向心力公式得
F-Mg=M![]() ③
③
F=Mg+M![]() =5Mg=15mg
=5Mg=15mg
(3)在最高点速度为零,向心加速度也就为零,设管受杆的力F′的方向向下,由向心力公式得Mg+F=0
F=-Mg (或直接设向上, 得F=Mg)
即杆管的作用力大小为Mg,方向与所设相反,即是竖直向上的支持力。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 (选修3-5)
(选修3-5)


 U→
U→ Th+
Th+ He属于裂变
He属于裂变
