题目内容
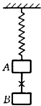如图所示，一根轻质弹簧固定在天花板上，下端系着质量为m的物体A，A的下面再用细绳挂另一质量也为m的物体B．平衡时将绳剪断，在此瞬时，A和B的加速度大小分别等于
- A.aA=g，aB=0
- B.aA=g，aB=g
- C.aA=g，aB=2g
- D.aA=0，aB=g．
B
分析：本题考查了瞬间加速度的计算，弹簧弹力不能发生突变，在剪短瞬间仍然保持原来的大小和方向；而细绳的弹力会发生突变，在剪断瞬间会突然改变；根据牛顿第二定律进行求解．
解答：剪断细线前，对AB整体受力分析，受到总重力和弹簧的弹力而平衡，故F=2mg；
剪断细线的瞬间，对A而言，受弹簧的弹力和重力，根据牛顿第二定律有：F-mg=maA，aA=g，方向向上．
对B，剪断细线的瞬间，仅受重力，根据牛顿第二定律知，aB=g，方向向下．故B正确，A、C、D错误．
故选B．
点评：本题是力学中的瞬时问题，关键是先根据平衡条件求出各个力，然后根据牛顿第二定律列式求解加速度；同时要注意轻弹簧的弹力与形变量成正比，来不及突变，而细线的弹力可以突变．
分析：本题考查了瞬间加速度的计算，弹簧弹力不能发生突变，在剪短瞬间仍然保持原来的大小和方向；而细绳的弹力会发生突变，在剪断瞬间会突然改变；根据牛顿第二定律进行求解．
解答：剪断细线前，对AB整体受力分析，受到总重力和弹簧的弹力而平衡，故F=2mg；
剪断细线的瞬间，对A而言，受弹簧的弹力和重力，根据牛顿第二定律有：F-mg=maA，aA=g，方向向上．
对B，剪断细线的瞬间，仅受重力，根据牛顿第二定律知，aB=g，方向向下．故B正确，A、C、D错误．
故选B．
点评：本题是力学中的瞬时问题，关键是先根据平衡条件求出各个力，然后根据牛顿第二定律列式求解加速度；同时要注意轻弹簧的弹力与形变量成正比，来不及突变，而细线的弹力可以突变．
练习册系列答案
阅读快车系列答案
相关题目
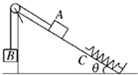如图所示，固定斜面的倾角θ=30°，物体A与斜面之间的动摩擦因数为μ=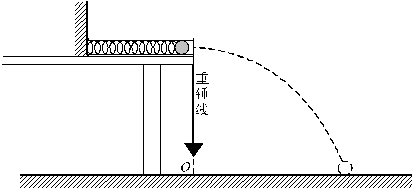
如图所示，在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上，球与墙之间有一根被压缩的轻质弹簧．当烧断细线时，小球被弹出，小球落地时的速度方向与水平方向成60°角，则弹簧被压缩时具有的弹性势能为（g=10m/s2）（ ）
如图所示，在高h为5m的光滑平台上有一个质量为0.2kg的小球被一细线拴在墙上，球与墙之间有一根被压缩的轻质弹簧，当烧断细线时．小球被弹出，小球落地时的速度方向与水平方向成45°．求