题目内容
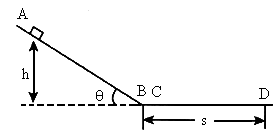
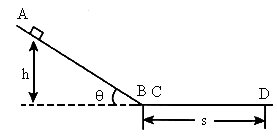
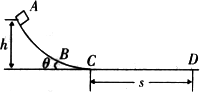
如图，ABCD是一段竖直平面内的光滑轨道，AB段与水平面成α角，CD段与水平面成β角，其中BC段水平，且其长度大于l．现有两小球P、Q，质量分别是2m、m，用一长为l的轻质直杆连结，将P、Q由静止从高Ⅳ处释放，在轨道转折处用光滑小圆弧连接，不考虑两小球在轨道转折处的能量损失，则小球P滑上CD轨道的最大高度h为（ ）
分析：根据两球及轻杆组成的系统机械能守恒，列式即可求得h．
解答：解：取水平面为参考平面，根据机械能守恒得
mgH+2mg（H+lsinα）=2mgh+mg（h+lsinβ）
解得 h=H+
故选B
mgH+2mg（H+lsinα）=2mgh+mg（h+lsinβ）
解得 h=H+
| l(2sinα-sinβ) |
| 3 |
故选B
点评：本题是系统的机械守恒问题，要注意选取参考平面，确定小球的高度．
练习册系列答案
阅读快车系列答案
相关题目
如图所示是一种磁动力电梯的模拟机，即在竖直平面内有两根很长的平行竖直轨道，轨道间有垂直轨道平面的匀强磁场B1和B2，且B1和B2的方向相反，B1=B2=1T，电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内（电梯桥厢在图中未画出），并且与之绝缘．电梯载人时的总质量为m=5×103kg，所受阻力大小为Ff=500N，金属框垂直轨道的边长为Lcd=2m，两磁场的宽度均与金属框的边长Lac相同，金属框整个回路的电阻为R=1.0×10-3Ω，问：
)