题目内容
11.月球是地球的天然卫星,可视为绕地球做匀速圆周运动.我国发射的“嫦娥二号”在月球表面附近绕月做匀速圆周运动.若利用“嫦娥二号”的周期T,万有引力常量为G,设月球和地球均为均匀球体,可估算出( )| A. | 地球的质量 | B. | 地球的密度 | C. | 月球的质量 | D. | 月球的密度 |
分析 根据万有引力提供向心力只能求解中心天体的质量,“嫦娥二号”在月球表面附近绕月做匀速圆周运动,根据万有引力提供向心力求出月球质量的表达式,根据已知条件判断能否求出质量,再根据密度公式判断能否求出月球密度.
解答 解:A、根据万有引力提供向心力只能求解中心天体的质量,所以无法求解地球的质量,更无法求解地球密度,故AB错误;
C、“嫦娥二号”在月球表面附近绕月做匀速圆周运动,设月球的质量为M,月球的半径为r,根据万有引力提供向心力得:
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$
解得:M=$\frac{4{π}^{2}{r}^{3}}{{GT}^{2}}$,由于不知道月球半径,所以无法求解月球质量,故C错误;
D、月球密度$ρ=\frac{M}{V}=\frac{\frac{4{π}^{2}{r}^{3}}{{GT}^{2}}}{\frac{4}{3}π{r}^{3}}=\frac{3π}{G{T}^{2}}$,知道周期,可以求出月球密度,故D正确.
故选:D
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、在星球表面万有引力等于重力,2、万有引力提供向心力,并能灵活运用,注意根据万有引力提供向心力只能求解中心天体的质量,难度适中.

练习册系列答案
相关题目
1.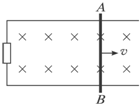 如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )
如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )
 如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )
如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过.下列说法中正确的是( )| A. | 因导体运动而产生的感应电动势称为感生电动势 | |
| B. | 动生电动势的产生与洛伦兹力有关 | |
| C. | 动生电动势的产生与电场力有关 | |
| D. | 动生电动势和感生电动势的产生原因是一样的 |
2.一个从静止开始做匀加速直线运动的物体,从开始运动起,连续通过三段位移的时间分别是1s、2s、3s,则这三段位移的长度之比分别是( )
| A. | 1:22:32 | B. | 1:23:33 | C. | 1:2:3 | D. | 1:3:5 |
6.(多选)关于气体分子运动的特点,下列说法正确的是( )
| A. | 气体分子之所以能充满空间,是因为气体分子间相互作用的引力和斥力十分微弱,气体分子可以在空间自由运动 | |
| B. | 每个气体分子的速率都相等 | |
| C. | 每个气体分子的速率都不等,速率很大和速率很小的分子数目很多 | |
| D. | 气体分子速率很大和速率很小的分子数目都很小 |
20. 如图,从斜面上的点以速度υ0水平抛出一个物体,飞行一段时间后,落到斜面上的B点,己知AB=75m,a=37°,不计空气阻力,下列说法正确的是(sin37°=0.6)( )
如图,从斜面上的点以速度υ0水平抛出一个物体,飞行一段时间后,落到斜面上的B点,己知AB=75m,a=37°,不计空气阻力,下列说法正确的是(sin37°=0.6)( )
 如图,从斜面上的点以速度υ0水平抛出一个物体,飞行一段时间后,落到斜面上的B点,己知AB=75m,a=37°,不计空气阻力,下列说法正确的是(sin37°=0.6)( )
如图,从斜面上的点以速度υ0水平抛出一个物体,飞行一段时间后,落到斜面上的B点,己知AB=75m,a=37°,不计空气阻力,下列说法正确的是(sin37°=0.6)( )| A. | 物体的位移大小为75m | B. | 物体飞行的时间为6s | ||
| C. | 物体的初速度v0大小为20m/s | D. | 物体在B点的速度大小为30m/s |
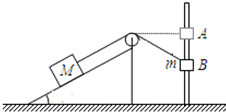 如图所示,质量为m和M的物块用不可伸长的轻绳连接,且M=4m,M放在倾角为θ=30°的固定光滑斜面上,而m能沿杆在竖直方向滑动,杆和滑轮中心间的距离为$\sqrt{3}$m,求当m由A点静止开始下落1m时的速度多大?(轮、绳质量及各种摩擦均不计,结果保留最简根式,取g=10m/s2)
如图所示,质量为m和M的物块用不可伸长的轻绳连接,且M=4m,M放在倾角为θ=30°的固定光滑斜面上,而m能沿杆在竖直方向滑动,杆和滑轮中心间的距离为$\sqrt{3}$m,求当m由A点静止开始下落1m时的速度多大?(轮、绳质量及各种摩擦均不计,结果保留最简根式,取g=10m/s2)
 如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且嵌入其中.已知物体B的质量为m,物体A的质量是m,子弹的质量是m.
如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹射中并且嵌入其中.已知物体B的质量为m,物体A的质量是m,子弹的质量是m.