题目内容
在研究性学习活动中,高二某班学生进行了如下实验:从入口S处送入某一频率的声音,通过左右两条管道路径SAT和SBT,声音传到了出口T处并可以从T处监听声音.右侧的B管可拉出或推入以改变B管的长度,开始时左右两侧管关于S、T对称,从S处送入某一频率的声音后,将B管逐渐拉出,当拉出长度为l时,第一次听到最小的声音.令声速为v,则该声音的频率为:( )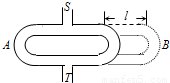
A.
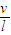
B.
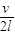
C.
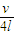
D.
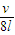
【答案】分析:当波峰与波谷相遇时,振动相互减弱.即听到声音最小.
解答:解:两列声波在出口T处发生干涉,
要第一次听到最低的声音,
需满足2l= ,
,
又因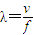 ,所以 f=
,所以 f=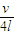
故C正确,ABD错误;
故选C
点评:考查波的叠加原理,当振动方向相同时,相互加强,当振动方向相反时,相互减弱.
还有一种较易理解的方法:
你画个正弦函数的图象,
可知要使波谷与波峰相遇
还得在原图象上向左会右移动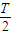 个单位
个单位
则SBT与SAT相差时间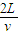 =
=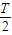
T=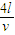
f=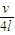 .
.
解答:解:两列声波在出口T处发生干涉,
要第一次听到最低的声音,
需满足2l=
 ,
,又因
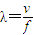 ,所以 f=
,所以 f=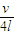
故C正确,ABD错误;
故选C
点评:考查波的叠加原理,当振动方向相同时,相互加强,当振动方向相反时,相互减弱.
还有一种较易理解的方法:
你画个正弦函数的图象,
可知要使波谷与波峰相遇
还得在原图象上向左会右移动
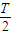 个单位
个单位则SBT与SAT相差时间
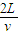 =
=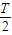
T=
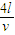
f=
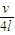 .
. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某同学在研究性学习活动中,研究课题是测定一高楼的高度.他将一台秤平放在电梯内,将一重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断地上升,最后停在最高层.在整个过程中,他根据秒表和台秤的示数,记录的数据如下表所示.假设在每一个时间段内台秤的示数是稳定不变的,其中0—3 s段,由于时间太短,他来不及将台秤的示数记录下来.g取10 m/s2,求:
(1)0—3 s时间段内台秤的示数.
(2)画出电梯上升过程的v-t图象,并求出第一层到最高层的楼高.
时间段(s) | 台秤示数(kg) |
电梯启动前 | 5.0 |
0—3.0 |
|
3.0—13.0 | 5.0 |
13.0—19.0 | 4.6 |
19.0 s以后 | 5.0 |
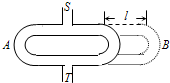 (2005?淮安模拟)在研究性学习活动中,高二某班学生进行了如下实验:从入口S处送入某一频率的声音,通过左右两条管道路径SAT和SBT,声音传到了出口T处并可以从T处监听声音.右侧的B管可拉出或推入以改变B管的长度,开始时左右两侧管关于S、T对称,从S处送入某一频率的声音后,将B管逐渐拉出,当拉出长度为l时,第一次听到最小的声音.令声速为v,则该声音的频率为:( )
(2005?淮安模拟)在研究性学习活动中,高二某班学生进行了如下实验:从入口S处送入某一频率的声音,通过左右两条管道路径SAT和SBT,声音传到了出口T处并可以从T处监听声音.右侧的B管可拉出或推入以改变B管的长度,开始时左右两侧管关于S、T对称,从S处送入某一频率的声音后,将B管逐渐拉出,当拉出长度为l时,第一次听到最小的声音.令声速为v,则该声音的频率为:( )

