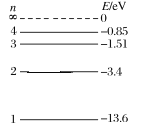
��Ŀ����
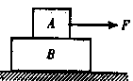
����Ŀ����ͼ��ʾ������ΪM��1kg���㹻����ľ�徲ֹ�ڹ⻬ˮƽ���ϣ�����һ����Ϊm��0.5kg��С���飨����Ϊ�ʵ㣩��v0��3m/s�ij��ٶȴ������ľ���ϱ������ľ�壬����ľ����ǰ��������֪������ľ���ϱ����Ķ�Ħ����������0.1���������ٶ�gȡ10m/s2����
��1���������ľ��ʱ��ľ�塢������Եļ��ٶȴ�С��
��2��������ľ��ﵽ�Ĺ�ͬ�ٶ�v�Ĵ�С��
��3����ľ��ij������ޣ���С�������ľ������ͬʱ��ľ����ʩ��һ�����ҵĺ���F��1.5N��Ҫ��֤С���鲻����ľ�壬��ľ��ij�������Ϊ���

���𰸡���1��1m/s2��0.5m/s2����2��1m/s����3��1.5m��
��������
(1)������֪������������ͼ��ʾ��![]()
�Ի��飬����ţ�ٵڶ����ɵã���mg=ma��
��ã�
a��=��g=1m/s2
��ľ��Ϊ�о�������ţ�ٵڶ������У���mg=Ma��
�ɵó�ľ��ļ��ٶ�Ϊ��
a��=0.5m/s2
(2)����Ի��������У�С�������ȼ����˶���ľ�����ȼ����˶����辭ʱ��t������ͳ�ľ��ﵽ��ͬ�ٶ�v�����У�
v=v0-a��t=a��t
�������ݿɵã�
t=1s
v=1m/s
(3)��ľ��������������ţ�ٵڶ������У�F1+��mg=Ma��1
��ã�
a��1=2m/s2
С������ľ����ٶ���ͬʱ��С����ǡ����ľ����Ҷˣ���ʱ��ľ�峤������Сֵ��λ�ƹ�ϵ��ͼ��ʾ��
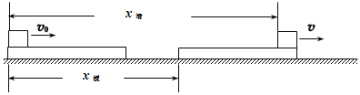
����
v0��a��t1��a��1t1
![]()
������ʽ�ɵã�
L��1.5m
��Ҫ��֤С���鲻����ľ�壬ľ��ij�������Ҫ1.5m��

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�