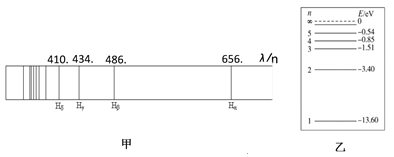
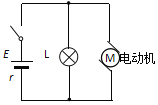
��Ŀ����
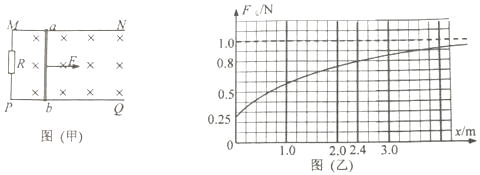
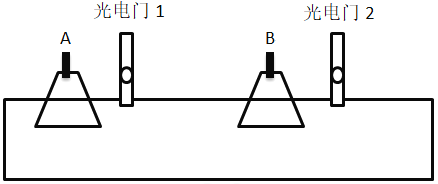
����Ŀ��ij��ȤС�������һ����߹��ģ����ͼ����ʾ����һ����Ϊm��0.5kg�����С����������Ϊ�ʵ㣩����P�㣬�õ���װ�ý���Ӿ�ֹ����������������ȫת��ΪС����ʼ���ܣ�ʹ�����Ű뾶Ϊr��1.0m�Ĺ⻬Բ����ֱ���OAO���˶������С����ˮƽ��PB������Ϊ������������0.5����gȡ10m/s2����PB��16.0m��OΪPB�е㡣B���Ҳ���һ����h��1.25m����L��2.0m�ĺ�������
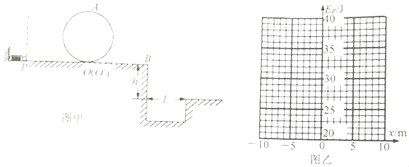
��1��ҪʹС��ǡ����Խ��Բ�ι������ߵ�A��С����O���ܵ���������Ĵ�С��
��2��Ҫ��С���ܰ�ȫԽ��A�㣬����B��ƽ��Խ���������ɵĵ�����������Ϊ���٣�
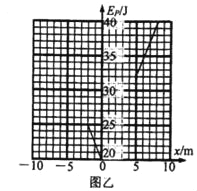
��3�����ڵ������ڣ����ɵ����������Epm��40J����O��Ϊ����ԭ�㣬OBΪx�ᣬ��O��B����Ϊ��������ͼ�������ϻ���С���ܽ���Բ�ι���Ҳ�����������£����ɵ�������Ep��С��ֹͣλ������x��ϵͼ��
���𰸡���1��ҪʹС��ǡ����Խ��Բ�ι������ߵ�A��С����O���ܵ���������Ĵ�С��30N����2��Ҫ��С���ܰ�ȫԽ��A�㣬����B��ƽ��Խ���������ɵĵ�����������Ϊ44J��
��3��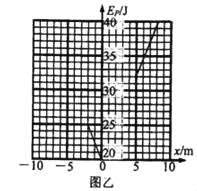
��������
��1��С��ǡ�þ���A��ʱ���У�![]()
�� ![]()
��С����O��A���̣����ݶ��ܶ������У�![]()
��� v0��5![]() m/s
m/s
С����O��ʱ����ţ�ٵڶ����ɵ� ![]()
������ã�FN��6mg��30N
��2��Ҫ������Խ��A�㣬v0��5![]() m/s
m/s
P��O��Ep��1��kmgxPO��![]() mv02��0
mv02��0
�� Ep��1��32.5J
Ҫ������ƽ���˶���Խ����������
L��vBt
h��![]() gt2
gt2
�ɵ� vB��4m/s
�ɶ��ܶ������� Ep��2��kmgxPB��![]() mvB2��0
mvB2��0
��� Ep��2��44J
�������������ɵĵ�����������Ϊ44J��
��3���������ۣ���Ϊ�������Ϊ40J������С�������˶���B�㣬�ز�ƽ�ס�
���1����Խ��A�㣬�������� 32.5J��Ep��1��40J��
��Ep��1��kmgx1��0��0���� 13m��x1��16m��
����ΪO��������ԭ�㣬����ʵ������ֵΪ 5m��x11��8m��
���2��ǡ�ܵ���Բ���Բ�ĵȸߴ�����Ep��2��kmgxPO��mgr��0��0���� Ep��2��25J
mgr��kmgx21���� x21��2m
����ΪO��Ϊ����ԭ�㣬����ʵ������ֵΪ x21����2m
ǡ�ܽ���Բ�������Ep��2��kmgxPO��0��0���� Ep��2��20J����ʱ����ֵΪ0
�ɶ��ܶ�������ʽ��֪��Ep����x�����Ժ���ͼ����ͼ��

 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�