Question

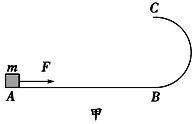
【题目】如图所示，将物块M无初速度的放在顺时针匀速传送的传送带的A点，已知传送带速度大小v=4m/s，AB=2m，BC=5m，M与传送带的动摩擦因数μ=0.5，试求物块由A运动到C点共需要多长时间．（M经过B点时速度大小不变，方向沿着BC方向；滑轮的半径很小，可忽略；g取10m/s2 ， sin37°=0.6，cos37°=0.8）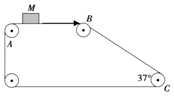

Answer 1

【答案】解：物体在传送带的A点，开始一段时间内受到向前的摩擦力作用做匀加速直线运动，

加速度为：a1= =μg=5m/s2

加速所用时间为t1= =0.8 s

物体做匀加速直线运动的位移为s1= =1.6 m

匀速运动的时间为t2= =0.1s

物体在BC段做匀加速直线运动，设这段加速度大小为a2，由受力情况及牛顿第二定律可知，mgsin 37°﹣μmgcos 37°=ma2

解得a2=2 m/s2

运动的位移为s2=BC=vt3+

解得 t3=1.0 s

故物块M运动到C所需时间为t=t1+t2+t3=1.9s

答：物体A运动到c点所需时间为1.9s．

【解析】物体在AB段，根据牛顿第二定律和运动学公式求出匀加速直线运动和匀速直线运动的时间，在BC段物体做匀加速直线运动，根据受力分析求出加速度，在结合运动学公式从而求得BC段上的时间，从而求出物体从A点运动到B点再到C点一共所用的时间．