题目内容
6.一列火车质量是1000t,由静止开始以额定功率沿平直轨道向某一方向运动,经1min前进900m时达到最大速度,设火车所受阻力恒定为车重的0.05倍,求:(g=10m/s2)(1)火车行驶的最大速度;
(2)火车的额定功率.
分析 (1)从静止开始到达到最大速度的过程中运用动能定理可以得到一个方程,再结合P额=fvm,即可求得最大速度;
(2)火车的额定功率可以根据P额=fvm求得.
解答 解:(1)从静止开始到达到最大速度的过程中,由动能定理得:
Pt-fx=$\frac{1}{2}$mvm2-0,
当牵引力等于阻力时,火车速度达到最大值,所以可得:
P额=Fvm=fvm=kmgvm
联列以上两式代入数据解得火车行驶的最大速度为:vm=30m/s
(2)火车的额定功率为:P额=kmgvm=0.05×1 000×103×10×30W=1.5×107W;
答:(1)火车行驶的最大速度为30m/s;
(2)火车的额定功率为1.5×107W.
点评 本题考查了功率公式P=Fv的应用,该题为机车启动问题,注意当牵引力等于阻力时速度达到最大值,该题难度适中.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
9. 一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )
一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )
 一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )
一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )| A. | 黑色的径迹将出现在木炭包的右侧 | |
| B. | 传送带运动的速度越小,径迹的长度越短 | |
| C. | 木炭包与传送带间动摩擦因数越大,径迹的长度越短 | |
| D. | 木炭包的质量越大,径迹的长度越短 |
11.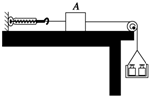 如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减
如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减
小为0.4kg,将会出现的情况是(g=10m/s2)( )
 如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减
如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减小为0.4kg,将会出现的情况是(g=10m/s2)( )
| A. | 物体A将具有向左运动的趋势 | B. | 弹簧秤的读数减小 | ||
| C. | 物体A将向左运动 | D. | 物体受到的摩擦力为2N |
18.有一个质量很小的小球A,用绝缘细线悬挂着,当用毛皮摩擦过的硬橡胶棒B靠近它时,看到他们相互吸引,接触后又相互排斥,则下列说法正确的是( )
| A. | 接触前,A、B一定带异种电荷 | B. | 接触前,A、B可能带异种电荷 | ||
| C. | 接触前,A球一定不带任何净电荷 | D. | 接触后,A球一定带电荷 |
15. 如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )
如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )
 如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )
如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )| A. | $\frac{G}{U}$ | B. | $\frac{G}{2U}$ | C. | $\frac{Gd}{U}$ | D. | $\frac{2Gd}{U}$ |