题目内容
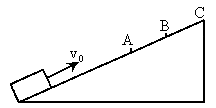
滑块以初速度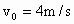 ,从光滑斜面的底端向上做匀减速运动,先后通过A、B点,到达斜面顶端C点时,速度恰好减小为零(如图所示),已知A、B相距d=0.75m,滑块通过A点和B点的瞬时速度
,从光滑斜面的底端向上做匀减速运动,先后通过A、B点,到达斜面顶端C点时,速度恰好减小为零(如图所示),已知A、B相距d=0.75m,滑块通过A点和B点的瞬时速度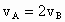 ,滑块由B到C的时间
,滑块由B到C的时间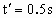 ,试问:
,试问:
(1)斜面多长?
(2)滑块在斜面上滑行的时间是多少?(至少用两种方法求解)
答案:略
解析:
解析:
|
方法 1:设斜面长为s,全程时间t,加速度大小为a,根据已知条件及匀变速直线运动规律可知:(1) 由B到C: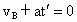 ,则 ,则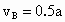 ; ;
(2) 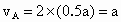 ; ;
(3) 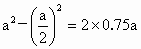 ;可得 ;可得 对全程而言: 对全程而言: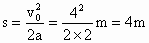 , ,
方法 2:(1)设滑块由A到B再到C,做匀减速运动;已知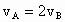 , , ;则 ;则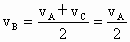 ,可见,滑块由A到B的时间,与由B到C的时间相等,都应为 ,可见,滑块由A到B的时间,与由B到C的时间相等,都应为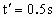 . .
(2) 已知A、B间距离为d=0.75m,则B、C间距离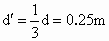
(3) 由A到C的平均速度等于中间时刻的瞬时速度,即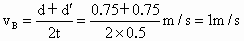
(4) 由 , ,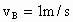 , ,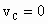 ,且时间间隔为 ,且时间间隔为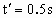 ,可知加速度的大小 ,可知加速度的大小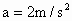 ,对全程而言: ,对全程而言: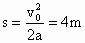 , ,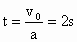
方法 3:由于斜面光滑,滑块向上做匀减速运动,滑块向下时做匀加速运动,加速度的大小是相等的,滑块向上与向下经过斜面上的同一点时速率也相等,所以,滑块从斜面的顶端C,由静止开始以加速度a向下做匀加速运动,先后通过B点与A点的速度 ;由C到B的时间与由B到A的时间相等,均为 ;由C到B的时间与由B到A的时间相等,均为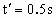 ,C到B的距离 ,C到B的距离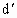 与B到A的距离d之比为 与B到A的距离d之比为 据此可以求得加速度a: 据此可以求得加速度a: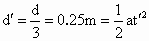
滑块向下滑动到斜面底端时速度大小为 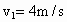 ,由此可以求得 ,由此可以求得
|

练习册系列答案
相关题目
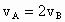

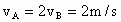
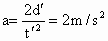
 .
.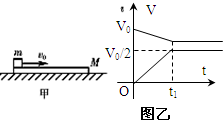 如图甲所示,质量为M的木板静止在光滑水平面上,一个质量为m的小滑块以初速度υ0从木板的左端向右滑上木板.滑块和木板速度随时间变化的图象如图乙所示,某同学根据图象作出如下一些判断,正确的是( )?
如图甲所示,质量为M的木板静止在光滑水平面上,一个质量为m的小滑块以初速度υ0从木板的左端向右滑上木板.滑块和木板速度随时间变化的图象如图乙所示,某同学根据图象作出如下一些判断,正确的是( )? 如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度v0从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,求
如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度v0从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,求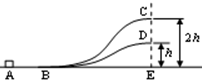 如图所示,让一滑块以初速度v0从A点出发,沿两个不同的轨道滑行分别到达C点或D点后水平抛出.已知两个轨道是固定的而且光滑,A、B、E在同一水平地面上,C、D、E在同一竖直线上,D点距地面的高度为h,C点高度为2h,重力加速度为g.
如图所示,让一滑块以初速度v0从A点出发,沿两个不同的轨道滑行分别到达C点或D点后水平抛出.已知两个轨道是固定的而且光滑,A、B、E在同一水平地面上,C、D、E在同一竖直线上,D点距地面的高度为h,C点高度为2h,重力加速度为g. 如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度v0从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,求滑块与水平轨道间的动摩擦因素.
如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度v0从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,求滑块与水平轨道间的动摩擦因素.