题目内容
1.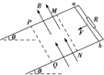 如图所示,间距为l=0.8m的两平行金属导轨倾斜放置,轨道与水平方向的夹角为θ=37°,导轨间接由一阻值R=1Ω的电阻,导轨电阻不计.一质量为m=0.2kg、电阻r=0.2Ω的金属棒ab垂直于导轨静止放在紧贴电阻R处,导轨间的矩形区域MNPQ内存在方向垂直导轨平面向上、磁感应强度大小为B=0.25T的有界匀强磁场,磁场宽度为d=0.85m,电阻R与边界MN之间的距离为s=0.72m,金属棒与两导轨间的动摩擦因数均为μ=0.5.现让金属棒ab在平行于倾斜轨道向下的外力F的作用下,由静止开始匀加速运动并穿过磁场,加速度大小为a=4m/s2,取g=10m/s2,sin37°=0.6,cos37°=0.8,则以下说法中正确的是( )
如图所示,间距为l=0.8m的两平行金属导轨倾斜放置,轨道与水平方向的夹角为θ=37°,导轨间接由一阻值R=1Ω的电阻,导轨电阻不计.一质量为m=0.2kg、电阻r=0.2Ω的金属棒ab垂直于导轨静止放在紧贴电阻R处,导轨间的矩形区域MNPQ内存在方向垂直导轨平面向上、磁感应强度大小为B=0.25T的有界匀强磁场,磁场宽度为d=0.85m,电阻R与边界MN之间的距离为s=0.72m,金属棒与两导轨间的动摩擦因数均为μ=0.5.现让金属棒ab在平行于倾斜轨道向下的外力F的作用下,由静止开始匀加速运动并穿过磁场,加速度大小为a=4m/s2,取g=10m/s2,sin37°=0.6,cos37°=0.8,则以下说法中正确的是( )| A. | 金属棒ab刚进入磁场时的速度大小为2.4m/s | |
| B. | 若从金属棒ab进入磁场开始计时,则金属棒在磁场中运动的时间内,外力F随时间的变化关系为F=$\frac{1}{2}$+$\frac{t}{6}$(N) | |
| C. | 金属棒ab在穿过磁场的过程中外力F做的功大于克服安培力所做的功 | |
| D. | 金属棒ab刚进入磁场的瞬间,电阻R的热功率为0.192W |
分析 分析导体棒的运动过程,利用运动学公式、牛顿第二定律以及能量的转化和守恒规律进行分析即可求解.
解答 解:A、由运动学公式可得:
v2=2as
解得:v=$\sqrt{2as}$=$\sqrt{2×4×0.72}$=2.4m/s;
B、由牛顿第二定律可知:
F+mgsin37°-μmgcos37°=ma;
解得,F=0.4N;
进入磁场后仍做匀加速运动,则有:
F+mgsin37°-μmgcos37°-$\frac{{B}^{2}{L}^{2}at}{R+r}$=ma;
解得:F=0.4+0.13t;故B错误;
C、金属棒在穿出磁场的过程中,拉力、重力、摩擦力及安培力做功;由于拉力一定大于安培力;故拉力做的功大于克服安培力所做的功;故C正确;
D、金属棒ab刚进入磁场的瞬间,电阻R的热功率为P=I2R=($\frac{BLv}{r+R}$)2R=($\frac{0.25×0.8×2.4}{1.2}$)2×1=0.16W;故D错误;
故选:AC.
点评 本题考查导体切割磁感线中的受力及能量转化问题,要注意明确运动过程的分析,并根据运动过程利用所学物理规律进行分析求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.关于力对物体做功的以下说法,正确的是( )
| A. | 力越大,力对物体做功越大 | |
| B. | 物体做圆周运动时,向心力对物体不做功 | |
| C. | 静摩擦力不可能对物体做功 | |
| D. | 作用力对物体做功,反作用力也一定对物体做功 |
13.关于点电荷的说法,正确的是( )
| A. | 只有体积很小的带电体,才能作为点电荷 | |
| B. | 体积很大的带电体一定不能看作点电荷 | |
| C. | 当带电体带电量很少时,可看成点电荷 | |
| D. | 一个带电体能否看成点荷,要看所研究的问题 |
10.如图甲所示是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列判断中正确的是( )
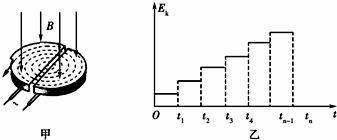

| A. | 在Ek t图中应有t4-t3<t3-t2<t2-t1 | |
| B. | 高频电源的变化周期应该等于tn-tn-1 | |
| C. | 当电源电压减小为$\frac{U}{2}$时,粒子加速次数增多,粒子最大动能增大 | |
| D. | 想粒子获得的最大动能越大,可增加D型盒的面积 |
11.质点做匀加速直线运动,初速度为v0=2m/s,加速度为a=0.1m/s2,则( )
| A. | 质点第4s末的速度为2.4m/s | |
| B. | 每经过2s时间,物体速度就增大2.2m/s | |
| C. | 质点加速度一直增大 | |
| D. | 质点速度随时间均匀增大 |

 如图所示是一种质谱仪的工作原理图,从粒子源产生的带电粒子经电压为U的加速电场加速后进入磁感应强度大小为B的匀强磁场,经磁场偏转后打在底片上的A点,若粒子的质量为m、带电荷量为q,进入加速电场时的初速度近似为零,OA之间的距离为x,粒子重力不计,则下列图象中能正确反映U与x之间的函数关系的是( )
如图所示是一种质谱仪的工作原理图,从粒子源产生的带电粒子经电压为U的加速电场加速后进入磁感应强度大小为B的匀强磁场,经磁场偏转后打在底片上的A点,若粒子的质量为m、带电荷量为q,进入加速电场时的初速度近似为零,OA之间的距离为x,粒子重力不计,则下列图象中能正确反映U与x之间的函数关系的是( )