题目内容
6.碳14(${\;}_{6}^{14}$C)是宇宙中的高能量中子碰撞空气中的氮原子后形成的,它很容易发生β衰变,变成一个新核,则该衰变的核反应方程为${\;}_{6}^{14}$C→${\;}_{7}^{14}$N${+}_{-1}^{0}$e;碳14可以用来测定古生物体的年代,当生物体死亡后,其机体内的碳14将会发生β衰变,导致其含量不断减少,已知碳14发生β衰变的半衰期为5730年,若测得一具古生物遗骸中碳14含量只有活体中的25%,则该遗骸距今约有11460年.分析 根据电荷数守恒、质量数守恒写出核反应方程;经过一个半衰期,有半数发生衰变,通过剩余的量确定半衰期的次数,从而求出遗骸距今约有多少年.
解答 解:根据电荷数守恒、质量数守恒得,${\;}_{6}^{14}$C→${\;}_{7}^{14}$N${+}_{-1}^{0}$e.
经过一个半衰期,有半数发生衰变,测得一古生物遗骸中的C含量只有活体中的25%,
根据($\frac{1}{2}$)n=$\frac{1}{4}$
得,n=2,即经过2个半衰期,
所以t=2×5730=11460年.
故答案为:${\;}_{6}^{14}$C→${\;}_{7}^{14}$N${+}_{-1}^{0}$e;11460.
点评 解决本题的关键知道在核反应中电荷数守恒、质量数守恒,以及知道半衰期的定义.

练习册系列答案
相关题目
16. 电场中某区域的电场线分布如图所示A、B为电场中的两点,若以EA、EB分别表示A、B两点的场强,φA、φB分别表示A、B两点的电势,则以下结论中正确的是( )
电场中某区域的电场线分布如图所示A、B为电场中的两点,若以EA、EB分别表示A、B两点的场强,φA、φB分别表示A、B两点的电势,则以下结论中正确的是( )
 电场中某区域的电场线分布如图所示A、B为电场中的两点,若以EA、EB分别表示A、B两点的场强,φA、φB分别表示A、B两点的电势,则以下结论中正确的是( )
电场中某区域的电场线分布如图所示A、B为电场中的两点,若以EA、EB分别表示A、B两点的场强,φA、φB分别表示A、B两点的电势,则以下结论中正确的是( )| A. | EA>EB,φA>φB | B. | EA<EB,φA<φB | C. | EA>EB,φA<φB | D. | EA<EB,φA>φB |
1.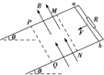 如图所示,间距为l=0.8m的两平行金属导轨倾斜放置,轨道与水平方向的夹角为θ=37°,导轨间接由一阻值R=1Ω的电阻,导轨电阻不计.一质量为m=0.2kg、电阻r=0.2Ω的金属棒ab垂直于导轨静止放在紧贴电阻R处,导轨间的矩形区域MNPQ内存在方向垂直导轨平面向上、磁感应强度大小为B=0.25T的有界匀强磁场,磁场宽度为d=0.85m,电阻R与边界MN之间的距离为s=0.72m,金属棒与两导轨间的动摩擦因数均为μ=0.5.现让金属棒ab在平行于倾斜轨道向下的外力F的作用下,由静止开始匀加速运动并穿过磁场,加速度大小为a=4m/s2,取g=10m/s2,sin37°=0.6,cos37°=0.8,则以下说法中正确的是( )
如图所示,间距为l=0.8m的两平行金属导轨倾斜放置,轨道与水平方向的夹角为θ=37°,导轨间接由一阻值R=1Ω的电阻,导轨电阻不计.一质量为m=0.2kg、电阻r=0.2Ω的金属棒ab垂直于导轨静止放在紧贴电阻R处,导轨间的矩形区域MNPQ内存在方向垂直导轨平面向上、磁感应强度大小为B=0.25T的有界匀强磁场,磁场宽度为d=0.85m,电阻R与边界MN之间的距离为s=0.72m,金属棒与两导轨间的动摩擦因数均为μ=0.5.现让金属棒ab在平行于倾斜轨道向下的外力F的作用下,由静止开始匀加速运动并穿过磁场,加速度大小为a=4m/s2,取g=10m/s2,sin37°=0.6,cos37°=0.8,则以下说法中正确的是( )
 如图所示,间距为l=0.8m的两平行金属导轨倾斜放置,轨道与水平方向的夹角为θ=37°,导轨间接由一阻值R=1Ω的电阻,导轨电阻不计.一质量为m=0.2kg、电阻r=0.2Ω的金属棒ab垂直于导轨静止放在紧贴电阻R处,导轨间的矩形区域MNPQ内存在方向垂直导轨平面向上、磁感应强度大小为B=0.25T的有界匀强磁场,磁场宽度为d=0.85m,电阻R与边界MN之间的距离为s=0.72m,金属棒与两导轨间的动摩擦因数均为μ=0.5.现让金属棒ab在平行于倾斜轨道向下的外力F的作用下,由静止开始匀加速运动并穿过磁场,加速度大小为a=4m/s2,取g=10m/s2,sin37°=0.6,cos37°=0.8,则以下说法中正确的是( )
如图所示,间距为l=0.8m的两平行金属导轨倾斜放置,轨道与水平方向的夹角为θ=37°,导轨间接由一阻值R=1Ω的电阻,导轨电阻不计.一质量为m=0.2kg、电阻r=0.2Ω的金属棒ab垂直于导轨静止放在紧贴电阻R处,导轨间的矩形区域MNPQ内存在方向垂直导轨平面向上、磁感应强度大小为B=0.25T的有界匀强磁场,磁场宽度为d=0.85m,电阻R与边界MN之间的距离为s=0.72m,金属棒与两导轨间的动摩擦因数均为μ=0.5.现让金属棒ab在平行于倾斜轨道向下的外力F的作用下,由静止开始匀加速运动并穿过磁场,加速度大小为a=4m/s2,取g=10m/s2,sin37°=0.6,cos37°=0.8,则以下说法中正确的是( )| A. | 金属棒ab刚进入磁场时的速度大小为2.4m/s | |
| B. | 若从金属棒ab进入磁场开始计时,则金属棒在磁场中运动的时间内,外力F随时间的变化关系为F=$\frac{1}{2}$+$\frac{t}{6}$(N) | |
| C. | 金属棒ab在穿过磁场的过程中外力F做的功大于克服安培力所做的功 | |
| D. | 金属棒ab刚进入磁场的瞬间,电阻R的热功率为0.192W |
11.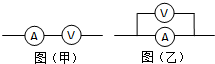 用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )
用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )
 用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )
用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )| A. | 图甲中电压表的指针偏角与电流表的相同 | |
| B. | 图甲中电压表的指针偏角比电流表的小 | |
| C. | 图乙中电压表的指针偏角比电流表的大 | |
| D. | 图乙中电压表的指针偏角比电流表的小 |
18.下列关于匀变速直线运动的说法,正确的是( )
| A. | 匀变速直线运动的υ-t图象是一条倾斜的直线 | |
| B. | 匀变速直线运动的x-t图象是一条倾斜的直线 | |
| C. | 匀变速直线运动是运动快慢相同的运动 | |
| D. | 匀变速直线运动是速度变化量相同的运动 |
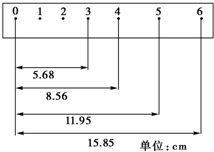 某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个测量点,每两个相邻的测量点之间还有四个点没标出,其部分相邻点间的距离如图所示,完成下列问题.
某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出0、1、2、3、4、5、6共7个测量点,每两个相邻的测量点之间还有四个点没标出,其部分相邻点间的距离如图所示,完成下列问题. 如图甲所示,质量分别为mA和mB的滑块A、B用轻质弹簧连接,当用大小为F1的水平力作用在滑块B上且使滑块A、B共同向右加速运动时,弹簧的伸长量为x;将此装置放在倾角为θ的斜面上,如图乙所示,当用大小为F2的拉力沿平行于斜面向上的方向作用在滑块B上且使滑块A、B共同沿斜面向上做加速运动时,弹簧的伸长量也为x,若两滑块与水平面、斜面间的动摩擦因数均为μ,则在两种情况下施加的拉力F1与F2之比为( )
如图甲所示,质量分别为mA和mB的滑块A、B用轻质弹簧连接,当用大小为F1的水平力作用在滑块B上且使滑块A、B共同向右加速运动时,弹簧的伸长量为x;将此装置放在倾角为θ的斜面上,如图乙所示,当用大小为F2的拉力沿平行于斜面向上的方向作用在滑块B上且使滑块A、B共同沿斜面向上做加速运动时,弹簧的伸长量也为x,若两滑块与水平面、斜面间的动摩擦因数均为μ,则在两种情况下施加的拉力F1与F2之比为( )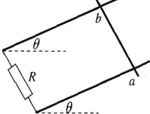 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值未知的电阻R.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值未知的电阻R.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.