题目内容
 (物理--选修3-3)
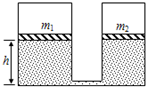
(物理--选修3-3)如图所示,两个可导热的气缸竖直放置,它们的底部都由一细管连通(忽略细管的容积).两气缸各有一个活塞,质量分别为m1和m2,活塞与气缸无摩擦.活塞的下方为理想气体,上方为真空.当气体处于平衡状态时,两活塞位于同一高度h.(已知m1=3m,m2=2m)
(1)在两活塞上同时各放一质量为m的物块,求气体再次达到平衡后两活塞的高度差(假定环境温度始终保持为T0).
(2)在达到上一问的终态后,环境温度由T0缓慢上升到T,试问在这个过程中,气体对活塞做了多少功?气体是吸收还是放出了热量?(假定在气体状态变化过程中,两物块均不会碰到气缸顶部).
分析:(1)不加物体时,两侧等高,说明活塞产生的压强相等;在两活塞上同时各放一质量为m的物块后,气体全部在左侧汽缸中,先求解出气压,然后根据玻意耳定律列式求解;
(2)等压膨胀过程,先根据盖-吕萨克定律列式求解末状态体积,然后求解气体对活塞做多少功,最后根据热力学第一定律判断气体的吸放热情况.
(2)等压膨胀过程,先根据盖-吕萨克定律列式求解末状态体积,然后求解气体对活塞做多少功,最后根据热力学第一定律判断气体的吸放热情况.
解答:解:(1)设左、右活塞的面积分别为A′和A,由于气体处于平衡状态,故两活塞对气体的压强相等,即:
=
由此得:A/=
A
在两个活塞上各加一质量为m的物块后,右边物体对活塞产生的压强较大,所以气体向左气缸移动,最终右活塞降至气缸底部,所有气体都在左气缸中.
在初态,气体的压强为
,体积为
Ah;
在末态,气体压强为
,体积为
Ax(x为左活塞的高度).
由玻意耳-马略特定律得:
5Ah=
3Ax
解得:x=
h
即两活塞的高度差为
h
(2)当温度由T0上升至T时,气体的压强始终为
,
设x′是温度达到T时左活塞的高度,
由盖?吕萨克定律得:x/=
x=
活塞对气体做的功为:W=Fs=4mg
h(
-1)=5mgh(
-1)
环境温度升高,则气体温度升高内能变大,又气体对活塞做功,根据热力学第一定律:在此过程中气体吸收热量.
答:(1)气体再次达到平衡后两活塞的高度差为
h.
(2)气体对活塞做了5mgh(
-1)的功,气体是吸收热量.
| 3mg |
| A/ |
| 2mg |
| A |
由此得:A/=
| 3 |
| 2 |
在两个活塞上各加一质量为m的物块后,右边物体对活塞产生的压强较大,所以气体向左气缸移动,最终右活塞降至气缸底部,所有气体都在左气缸中.
在初态,气体的压强为
| 2mg |
| A |
| 5 |
| 2 |
在末态,气体压强为
| 8mg |
| 3A |
| 3 |
| 2 |
由玻意耳-马略特定律得:
| mg |
| A |
| 4mg |
| 3A |
解得:x=
| 5 |
| 4 |
即两活塞的高度差为
| 5 |
| 4 |
(2)当温度由T0上升至T时,气体的压强始终为
| 8mg |
| 3A |
设x′是温度达到T时左活塞的高度,
由盖?吕萨克定律得:x/=
| T |
| T0 |
| 5Th |
| 4T0 |
活塞对气体做的功为:W=Fs=4mg
| 5 |
| 4 |
| T |
| T0 |
| T |
| T0 |
环境温度升高,则气体温度升高内能变大,又气体对活塞做功,根据热力学第一定律:在此过程中气体吸收热量.
答:(1)气体再次达到平衡后两活塞的高度差为
| 5 |
| 4 |
(2)气体对活塞做了5mgh(
| T |
| T0 |
点评:本题关键是明确气体经历等压过程,然后灵活地选择气体实验定律列方程求解,根据热力学第一定律判断吸放热情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 物理--选修3-3
物理--选修3-3 [物理-选修3-3]
[物理-选修3-3]