题目内容
【题目】如图所示,固定的光滑平台上固定有光滑的半圆轨道,轨道半径R=0.6 m.平台上静止着两个滑块A、B,mA=0.1 kg,mB=0.2 kg,两滑块间夹有少量炸药,平台右侧有一带挡板的小车静止在光滑的水平地面上,小车质量为M=0.3 kg,小车的上表面与平台的台面等高,小车的上表面的右侧固定一根轻弹簧.点燃炸药后,A、B分离瞬间滑块B以3 m/s的速度冲向小车.两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个滑块的速度方向在同一水平直线上,且g=10 m/s2.求:
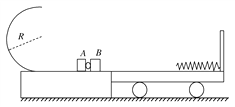
(1)滑块A能否从半圆轨道的最高点离开;
(2)滑块B滑上小车后的运动过程中弹簧的最大弹性势能。
【答案】(1)能 (2)0.54 J
【解析】本题考查动量守恒与曲线运动及机械能守恒相结合的问题。
(1)爆炸前后A、B组成的系统动量守恒,设爆炸后滑块A、B的速度大小分别为vA、vB,则![]()
解得vA=6 m/s
A在运动过程中机械能守恒,若A能到达半圆轨道最高点
由机械能守恒得![]()
解得![]()
滑块恰好通过最高点的条件是![]()
解得![]()
所以A能从半圆轨道最高点离开
(2)滑块B冲上小车后将弹簧压缩到最短时,弹簧具有最大弹性势能,此时B和小车具有相同速度,由动量守恒定律得![]()
由能量守恒定律得![]()
解得Ep=0.54 J.

练习册系列答案
相关题目